Gpy と Scikit-learn

Python でガウス過程を行うモジュールには大きく分けて2つが存在します。一つは Gpy (Gaussian Process の専門ライブラリ) で、もう一つは Scikit-learn 内部の Gaussian Process です。

この2つのモジュールでどのような違いがあるのかを以下の項目で比較していきます。

カーネルの種類, 可視化
- どんな種類のカーネルがあるのか
- 可視化は容易か
予測モデルの作成
- モデルの作成はどのように行うのか
- モデルの訓練方法, 結果の可視化方法はどうなっているか
事後分布からのサンプリング
- モデルの事後分布からのサンプリングを行えるか

使用した jupyter-notebook は以下の gist を参照してください。

カーネルの種類, 可視化

カーネルを定義して可視化する難易度を比較していきます。

scikit-learn

scikit-learn でガウス過程をする際には sklearn.gaussian_process を用います。カーネルの定義も同じ名前空間内に定義されていますので from sklearn.gaussian_process import kernels でインポートできます。今回は Gpy のカーネルもインポートしていたので as を指定していますが別にそのままでも問題ないです。

色々とカーネルは定義されています (公式サイトを参照してください)

が今回は中心から遠くなると小さい値になる RBF カーネルと ExpSineSquared カーネル ( Periodic Kernel と呼ぶのが普通のような気がしますが sklearn ではこう呼ばれているようです) をかけ合わせたものを可視化します.

from sklearn.gaussian_process import kernels as sk_kern

kern = sk_kern.RBF(length_scale=.5)
kern = sk_kern.ExpSineSquared() * sk_kern.RBF()

# ほかにも色々と種類はある。ドキュメント参照
# kern = sk_kern.RationalQuadratic(length_scale=.5)
# kern = sk_kern.ConstantKernel()
# kern = sk_kern.WhiteKernel(noise_level=3.)

# 可視化は定義されていないので自分で用意する必要あり
X = np.linspace(-2, 2, 100)
plt.plot(X, kern(X.reshape(-1, 1), np.array([[0.]])))

f:id:dette:20170529033631p:plain

GPyの場合

kern = GPy.kern.PeriodicExponential(lengthscale=.1, variance=3) * GPy.kern.Matern32(1)
# kern = GPy.kern.RatQuad(1, lengthscale=.5, variance=.3)
# kern = GPy.kern.White(input_dim=1)
kern.plot()

f:id:dette:20170529033651p:plain

kern = GPy.kern.Linear(input_dim=2) * GPy.kern.Matern52(input_dim=2)
kern.plot()

f:id:dette:20170529033708p:plain

違い

カーネルの数

GPy の方が用意されている関数の数が多いです。具体的には PeriodicExponential など周期性を持ったカーネルや Matern52 のようなカーネルも用意されています。

可視化

GPy には可視化用の関数 plot が用意されています。しかし Scikit-learn には同様のメソッドが無いため、自分で入力するベクトルを作る部分から書き下す必要があります。

定義方法

GPy においては、カーネルの定義の時点で、入力する特徴量の次元数 input_dim を指定する必要があります。カーネル計算のためのデータがあたえられれば、特徴量の次元数は自明に判明するため、この変数はやや冗長のようにも感じられます。一方 Scikit-learn ではカーネルの定義では純粋にカーネルの情報のみを入力すればよいです。

予測モデルの作成

Scikit-learn と GPy のそれぞれで、人工データに対する予測モデルを作っていきます。

データ作成

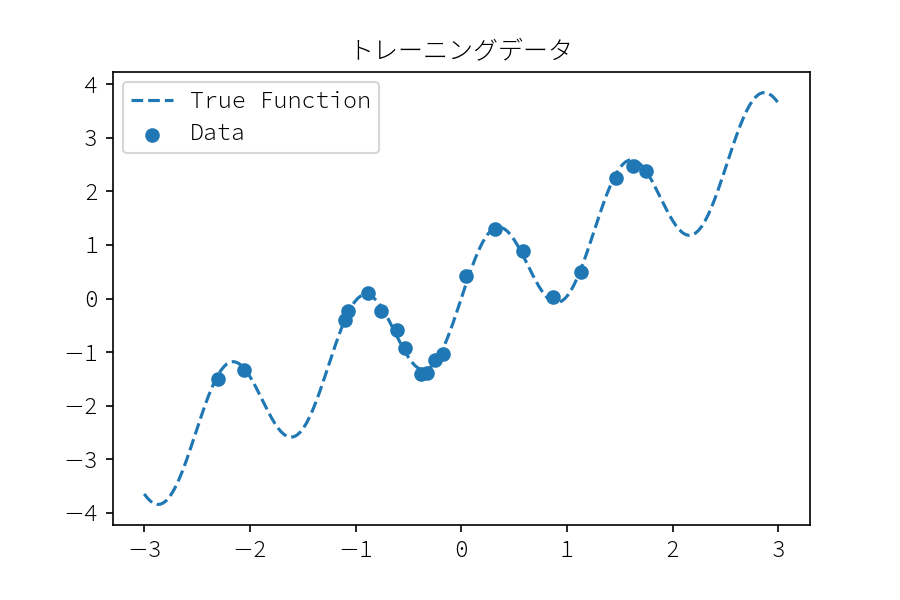
今回予測モデルに与える訓練データデータを作成します。正しい関数は $f(x) = x + \sin(5x) $ とし, 分散 .1 のガウス分布によるノイズを付与します。

def true_func(x):
    """
    正しい関数
    
    :param np.array x:
    :return: 関数値 y
    :rtype: np.array
    """
    y = x + np.sin(5 * x)
    return y

np.random.seed(1)
x_train = np.random.normal(0, 1., 20)
y_train = true_func(x_train) + np.random.normal(loc=0, scale=.1, size=x_train.shape)
xx = np.linspace(-3, 3, 200)
plt.scatter(x_train, y_train, label="Data")
plt.plot(xx, true_func(xx), "--", color="C0", label="True Function")
plt.legend()
plt.title("トレーニングデータ")
plt.savefig("training_data.png", dpi=150)

f:id:dette:20170529033728p:plain

Scikit-learn

まず Scikit-learn でモデルを作成します。

kernel = sk_kern.RBF(1.0, (1e-3, 1e3)) + sk_kern.ConstantKernel(1.0, (1e-3, 1e3)) + sk_kern.WhiteKernel()
clf = GaussianProcessRegressor(
    kernel=kernel,
    alpha=1e-10, 
    optimizer="fmin_l_bfgs_b", 
    n_restarts_optimizer=20,
    normalize_y=True)

パラメータ詳細

alpha:
- ガウス過程ではカーネルの逆行列を計算する必要があります。一般に実用上用いられるカーネル関数がつくる行列は、入力のベクトルの値がすべて異なる場合、数学的にはかならず正定値です。しかし、固有値の値が非常に小さくなる場合があり、この時逆行列の計算は数値的に不安定性となってしまいます。これを補正するための値が alpha で、行列に対角成分に alpha を持つ対角行列を加えることで、最小固有値の値が alpha よりもおおきくなるように補正し、計算安定性を確保します。
normalize_y: default True
- 予測変数の平均を 0 になるように正規化します。Gaussian Process の計算の際の数値的安定性担保のため行われます.
n_restarts_optimizer
- カーネルのハイパーパラメータを最適化する回数です。 0の場合1回の最適化で終わりますが、0以上が設定されると, 直前の最適化で得られた最適解を初期点として再び最適化を行います.

# X は (n_samples, n_features) の shape に変形する必要がある
clf.fit(x_train.reshape(-1, 1), y_train)

# パラメータ学習後のカーネルは self.kernel_ に保存される
clf.kernel_ # < RBF(length_scale=0.374) + 0.0316**2 + WhiteKernel(noise_level=0.00785)

# 予測は平均値と、オプションで 分散、共分散 を得ることが出来る
pred_mean, pred_std= clf.predict(x_test, return_std=True)

def plot_result(x_test, mean, std):
    plt.plot(x_test[:, 0], mean, color="C0", label="predict mean")
    plt.fill_between(x_test[:, 0], mean + std, mean - std, color="C0", alpha=.3,label= "1 sigma confidence")
    plt.plot(x_train, y_train, "o",label= "training data")

x_test = np.linspace(-3., 3., 200).reshape(-1, 1)
plot_result(x_test, pred_mean, pred_std)
plt.title("Scikit-learn による予測")
plt.legend()
plt.savefig("sklern_predict.png", dpi=150)

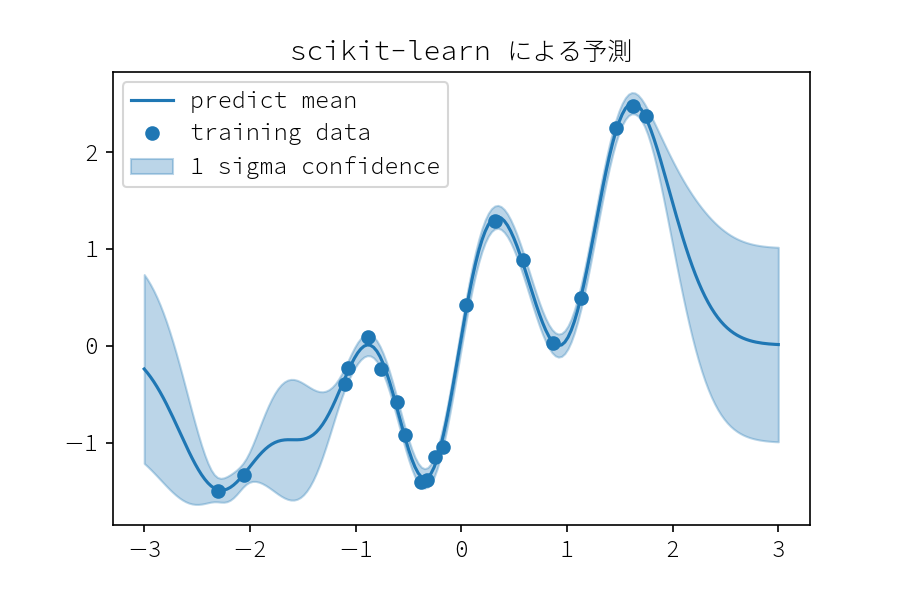
f:id:dette:20170529033748p:plain

GPy

次に GPy で予測モデルを作成していきます.

import GPy.kern as gp_kern
# kern = gp_kern.PeriodicMatern32(input_dim=1) * gp_kern.RBF(input_dim=1)
kern = gp_kern.RBF(input_dim=1) + gp_kern.Bias(input_dim=1)
kern = gp_kern.PeriodicExponential(input_dim=1)
gpy_model = GPy.models.GPRegression(X=x_train.reshape(-1, 1), Y=y_train.reshape(-1, 1), kernel=kern, normalizer=None)

パラメータ詳細

normalizer (default False)
- 予測変数 Y の正規化を決定する変数です。 None が与えられるとガウス正規化が行われます。
noise_var (default 1)
- データのノイズの分散を指定します. scikit-learn ではノイズは自分でカーネルに仕込む必要がありますが、 GPy.model.GPRegression ではデフォルトでノイズを考慮する用になっているため、カーネルにノイズを加える必要はありません。

fig = plt.figure(figsize=(6,8))
ax1 = fig.add_subplot(211)
gpy_model.plot(ax=ax1)  # 最適化前の予測
gpy_model.optimize()

ax2 = fig.add_subplot(212, sharex=ax1)
gpy_model.plot(ax=ax2)  # カーネル最適化後の予測

ax1.set_ylim(ax2.set_ylim(-4, 4))
ax1.set_title("GPy effect of kernel optimization")
ax1.set_ylabel("Before")
ax2.set_ylabel("After")
fig.tight_layout()
fig.savefig("GPy_kernel_optimization.png", dpi=150)

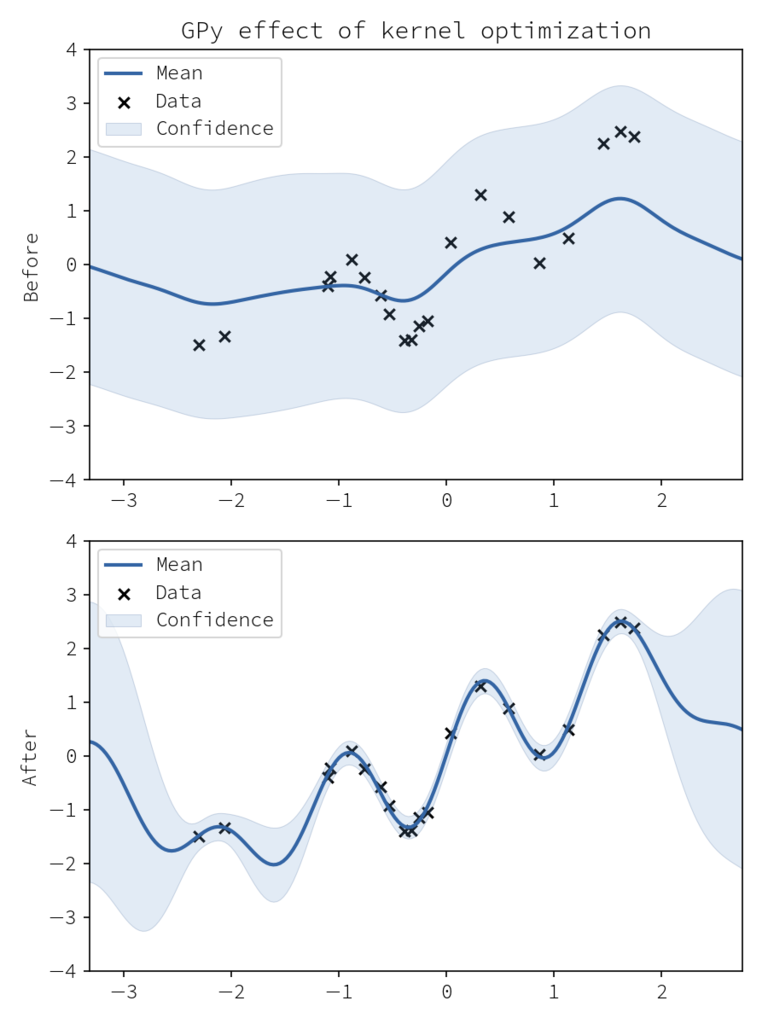
f:id:dette:20170529033803p:plain

# 最適化されたモデルの確認
print(gpy_model)

Name : GP regression
Objective : 6.799282795295307
Number of Parameters : 4
Number of Optimization Parameters : 4
Updates : True
Parameters:
  [1mGP_regression.                  [0;0m  |             value  |  constraints  |  priors
  [1mperiodic_exponential.variance   [0;0m  |     2.85057672019  |      +ve      |        
  [1mperiodic_exponential.lengthscale[0;0m  |    0.416248308257  |      +ve      |        
  [1mperiodic_exponential.period     [0;0m  |      11.478988407  |      +ve      |        
  [1mGaussian_noise.variance         [0;0m  |  0.00923971637791  |      +ve      |

pred_mean, pred_var = gpy_model.predict(x_test.reshape(-1, 1), )
pred_std = pred_var ** .5
plot_result(x_test, mean=pred_mean[:, 0], std=pred_std[:, 0])
plt.legend()
plt.title("GPyによる予測")
plt.savefig("GPy_predict.png", dpi=150)

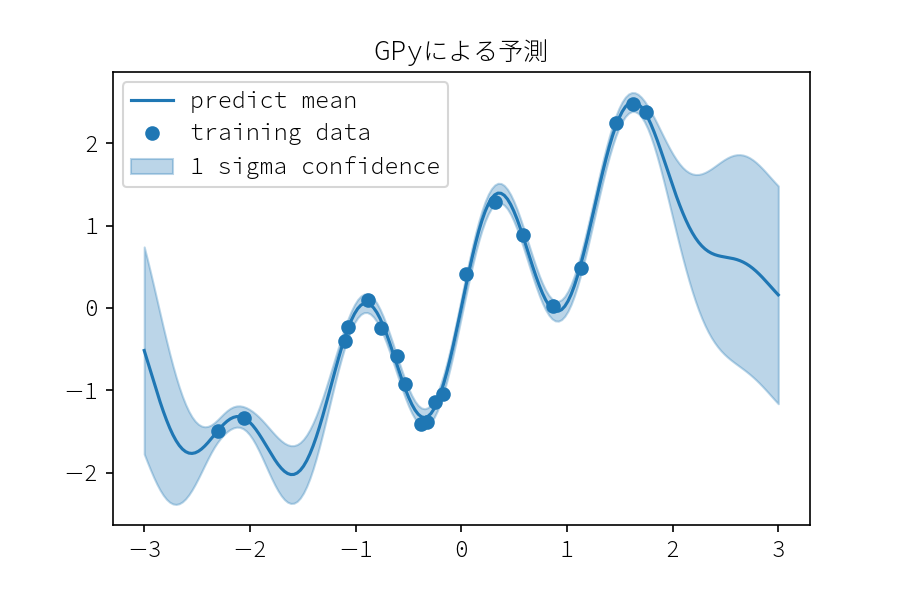
f:id:dette:20170529033824p:plain

事後分布からのサンプリング

scikit-learn には、そもそもサンプリングする関数が存在しません。 (事後分布の共分散を取得して, 自分でゴニョゴニョ計算してサンプリングする必要があります. )

一方 GPy では posterior_samples という関数が用意されており, これを用いて事後分布からのサンプリングを行うことができます. また posterior_samples_f を用いれば, 事後分布から確率過程をサンプルすることも可能です。以下では30個の確率過程をサンプリングして図示しています.

posterior = gpy_model.posterior_samples_f(x_test.reshape(-1, 1), size=30)

for i, pos in enumerate(posterior.T):
    label = None
    if i == 0:
        label = "posteror"        
    plt.plot(x_test[:, 0], pos, color="C0", alpha=.1, label=label)
plt.plot(x_train, y_train, "o")
plt.title("事後分布からのサンプリング")
plt.legend()
plt.savefig("posterior.png", dpi=150)

f:id:dette:20170529035551p:plain

以上をまとめましょう。

カーネルの定義, 可視化

カーネルの種類

GPy の方が多くのカーネルが用意されていますので、GPy > Scikit-learn といえるでしょう。しかし一方で生成時にデータの情報を入れ無くてはならないという冗長性があり、この点ではインスタンス生成時に純粋にカーネルに関する情報だけ入れれば良い Scikit-learn は綺麗です 🍺。

可視化

GPy >> Scikit-learn といえるでしょう. GPy にはカーネル関数はもちろんのこと、予測モデル自体にもplotする機能がついています。このため「今回のデータにはどういう周期性を持ったカーネルが良いか」などの検討を用意に行えます。また model.optimize を呼び出す前後での model.plot をすることで、最適化の妥当性のチェックをすぐさま行うことができます。

予測モデルの作成

事後分布平均と分散

事後分布の平均値と分散の取得はどちらのライブラリでも簡単に取得することができます。この点で違いは無いです。

手続き的な違い

GPyではインスタンス生成時にデータ X, y をわたし, model.optimize メソッドの呼び出し時に、カーネルのパラメータを最適化します。一方で, Scikit-learn ではインスタンス生成時には何も行わずインスタンス変数の初期化のみを行い, fit メソッドでデータ X, y をわたし, ここで同時にカーネルのパラメータ最適化を行っています。

事後分布からのサンプリング

Scikit-learn では一つの点での平均と分散を得ることはできますが、事後分布から確率過程をサンプリングすることはできません。一方で GPy では poseterior_samples, poseterior_samples_f を用いればかんたんに事後分布からのサンプルを行えます.

その他の違い

GPyにはシンプルなガウス過程を用いた回帰問題以外にも, 損失関数をポアソン分布に変更し、二次の意味でガウス分布として近似してやるポアソン回帰モデルなども作成することができ, 拡張性に長けています。*1

一方 Scikit-learn では回帰と分類のモデルのみで, 複雑な目的関数を扱う枠組みは用意されていません。

以上のことから

GPy
- カーネルの形状やモデルのフィッティングの確認を行いつつどのようなカーネルの設計にしていくのかを考えていきたい
- より複雑なモデルを定義したい
Scikit-learn
- もうどのカーネルを用いたら良いかがわかっていて特段可視化を重要視しない
- Gridsearch で最適なカーネルの組み合わせを調べたい

という使い分けをするのがよいと言えるでしょう。

*1:https://github.com/SheffieldML/notebook/blob/master/GPy/Poisson%20regression%20tutorial.ipynb

nykergoto’s blog

機械学習とpythonをメインに

Gpy vs scikit-learn: pythonでガウス過程回帰

Gpy と Scikit-learn

カーネルの種類, 可視化

scikit-learn

GPyの場合

違い

カーネルの数

可視化

定義方法

予測モデルの作成

データ作成

Scikit-learn

パラメータ詳細

GPy

パラメータ詳細

事後分布からのサンプリング

カーネルの定義, 可視化

カーネルの種類

可視化

予測モデルの作成

事後分布平均と分散

手続き的な違い

事後分布からのサンプリング

その他の違い