nykergoto’s blog

機械学習とpythonをメインに

トップ > 機械学習 > 特徴量選択アルゴリズム HSIC Lasso とその周辺を調べた

特徴量選択アルゴリズム HSIC Lasso とその周辺を調べた

機械学習 論文

先日、特徴量選択についてツイートしたところ Kaggle Master のアライさんに「HSIC Lassoはまさにぴったしなんではないでしょうか?」と教えていただきました。

HSIC Lasso は直前にあった統計学勉強会#2でのアライさんの発表資料でも取り上げられていたものです。 統計学勉強会は twitter から眺める程度で見ていたのですがとても盛り上がっていて楽しそうした。次回は是非参加したいと思っています🔥

connpass.com

www.slideshare.net

自分がこの分野に疎いのでただ使うだけじゃなくて中身の気持ちとか似た手法についても調べたいなと思い、いろいろと調べてみました。以下は HSIC Lasso を提案した論文 High-Dimensional Feature Selection by Feature-Wise Kernelized Lasso とそこで引用されている論文・資料などをまとめたものになります。

おことわり・説明していないこと

  • HSIC に関する詳しい説明
  • HSIC Lasso 以外の特徴選択手法に関する網羅的な説明
    • 論文中で触れられているもの程度しか紹介していませんので、網羅性はあまりないです
    • また筆者は特徴量選択手法に詳しい人間ではありませんので、誤りがあるかもしれません。おや?と思ったひとは元論文にあたっていただけると幸いです。

特徴量選択とはなにか

ある予測対象である目的変数 $y$ と、それに紐付いた $d$ 次元の特徴ベクトル $x \in \mathbb{R}^d$ があり、それが全部で $N$ 個ある状況を考えます。

一般的な機械学習では $x$ を入力とした時に $y$ を説明するような関数 $f$ を作成することが目標ですが、それとは別に $x$ のうちで有効なものはどれかを知りたい場合があります。例えば特徴量を観測するのがとてもコストが高くて、一部だけでなんとかやりたい時など、たくさんの特徴のうちどれが意味があるものかを知りたい状況は良くあります。

このように、入力された特徴量 $x$ のなかから、目的変数 $y$ を説明・予測するのに有効な特徴量の組を選ぶことを特徴量選択とよびます。

Lasso

もっとも有名な特徴選択アルゴリズムの一つに Lasso があります。Lasso は以下の最適化問題として記述することができます。

$$ \min_{\alpha \in {\mathbb{R}}^d } \frac{1}{2} || y - X^{\rm T} \alpha ||^2_2 + \lambda || \alpha ||_1 $$

ここで $y \in \mathbb{R}^n$、$X = [x_1, x_2, \cdots, x_n] \in \mathbb{R}^{d \times n}$ は目的変数・特徴量をデータの数 $n$ だけ並べたベクトルで $\alpha \in \mathbb{R}^d$ は特徴量の重みです。

第一項はデータへの当てはまりを表していて、第二項は正則化(重みへのペナルティ)になっています。Lasso は正則化項として L1 ノルムを使っているため L2 をつかう Ridge に比べてスパースな解が得られやすいというメリットがありますが、非線形性を捉えることができないという欠点を抱えています。

Instance-Wise Non-Linear Lasso

非線形性を捉えられるように改良したものとして、データ点ごと (instance-wise) な Lasso Instance-Wise Non-Linear Lasso があります。

$$ \min_{\beta \in {\mathbb{R}}^n } \frac{1}{2} || y - A \beta ||^2_2 + \lambda || \beta ||_1 $$

ここで $A \in \mathbb{R}^{n \times n}$ は $A_{i,j} = \phi(x_i)^{\rm T} \phi(x_j)$ で表される行列で $\phi(\cdot): \mathbb{R}^d \to \mathbb{R}^{d'}$ は特徴量 $x$ を $d'$ 次元のベクトルへ変換する非線形関数です。Lasso とデータへの当てはめる部分が異なっていて、特徴 $x$ を非線形変換したあと、すべてのデータ点との距離 (内積) へと変換する処理が入っています。

$\phi$ という非線形関数を組み込むことによって、特徴量の線形な関係以外も記述できるようになりますが、決定される重み $\beta$ は $n$ 個のデータ点に対する重み付けになっています。

要するに、どのデータ点からの距離が重要かはわかる (SVM でいうところの Support Vector がわかる ) のですが、どの特徴量が大事か? には答えてくれませんから、特徴量の選択としてもちいることはできません。

Feature-Wise Non-Linear Lasso (FVM: Feature Vector Machine)

上記のデータごとの非線形性を特徴点へと拡張したものが Feature-Wise Non-Linear Lasso (FVM) です。FVM はデータの空間ではなく、データ数 $n$ の次元からある別の次元 $p$ へと変換する非線形関数 $\phi(\cdot): \mathbb{R}^n \to \mathbb{R}^p$ で変換した空間上での距離を当てはまりの関数として用います。

$$ \min_{\alpha \in {\mathbb{R}}^d } \frac{1}{2} || \phi(y) - \Phi \alpha ||^2_2 + \lambda || \alpha ||_1 $$

ここで $\Phi = [\phi(u_1), \cdots, \phi(u_d)] \in \mathbb{R}^{p \times d}$ であり $u_k = [x_{k, 1}, x_{k, 2}, \cdots, x_{k, n}]$ はすべてのデータの第 $d$ 番目の特徴を並べたベクトルです。目的変数 $y$ も $\phi$ を使って変換しているため, データへの当てはまり部分が $p$ 次元上での L2 ノルムになっていることに注意してください。

最適化する重み $\alpha$ は $d$ 次元ですから、回帰係数として捉えることができ、これの大きい物を選ぶことで特徴量選択として用いることができます。

これを解く場合には、双対問題を考えることでカーネルトリックを使うことができます。したがって、内積 $\phi(x)^{\rm T} \phi(y)$ にあたるカーネル関数さえ用意すれば解くことができます。

双対空間上では $d \times d$次元のヘッセ行列の逆行列計算を行なうことになるため、データ $n$ が次元数 $d$ に比べて大きい時に有利な手法です。

FVM は非線形性を扱えてかつ特徴選択にも用いることもできる手法ですがいくつかの欠点も抱えています。

提案されたオリジナル論文では、カーネルとして相互情報量が使われていました。相互情報量をカーネルにもつヘッセ行列は正定値行列と限らず、双対問題は非凸最適化になり、解くことが難しいです。また先にデータ数が大きい時有利とかきましたが、反対に言えば特徴次元数が大きい時には不利になりますし、そのような場合にはヘッセ行列が singular になりやくこれまた解くことが難しいです。

また回帰・分類問題の種類によらずに、目的変数 $y$ を入力 $x$ を同じ非線形関数で変換する必要があるという構造上の欠点も抱えています。

HSIC Lasso

表題にもなっています HSIC Lasso は以下の目的関数を最適化することで、特徴量の重要度を算出します。

$$ \min_{\alpha \in {\mathbb{R}}^d } \frac{1}{2} || \tilde{L} - \sum_{k=1}^d \alpha_k \tilde{K}^k ||^2_{\rm Frob} + \lambda || \alpha ||_1 \\ s.t.\ \alpha_i \ge 0\ (i = 1,2,\cdots d) $$

Frob は行列の要素ごとのノルム(フロベニウスノルム)です。$L$, $K$ はそれぞれ予測値, 特徴量を変換したグラム行列で, $\tilde{L} = \Gamma L \Gamma$, $\tilde{K} = \Gamma K \Gamma$ のように中心化行列 $\Gamma = I_n - \frac{1}{n} 1_n 1_n^{\rm T}$ によって中心化が施されています。

出力 $y$ に対してグラム行列を定義しているので出力に対して非線形性を自然に組み込めていること、さらには入力に対して出力と別のグラム行列を定義していますので、入力の非線形性も捉えることができていそうな感じはしますね。

Note.1 中心化行列 (centering matrix)

中心化行列: https://en.wikipedia.org/wiki/Centering_matrix はいくつかの嬉しい性質を持った行列です。特徴のひとつに「あるベクトル $v$ に対して中心化行列 $\Gamma$ を掛け算するとベクトルの要素の平均値を引く演算になる (結果の平均値がゼロになって""中心化""される)」というものがあります。

$$ \Gamma v = v - \frac{1}{N} 1_N \sum_{n=1}^N v_n = v - \mu $$

ここで $\mu_i = 1/n \sum_{n=1}^N v_n$ で表される値。要するに $v$ の平均値で全部並べたベクトル。

HSIC Lasso を解釈する

提案手法のデータへの当てはまりの第一項を変形すると以下のようになります。

$$ \frac{1}{2} {\rm HSIC} (y, y) - \sum_{k=1}^{d} \alpha_k {\rm HSIC} (u_k, y) + \frac{1}{2} \sum_{k,l=1}^d \alpha_k \alpha_l {\rm HSIC} (u_k, u_l) $$

ここで現れている ${\rm HSIC} (u_k, y) = {\rm tr} (\tilde{K}^{(k)} \tilde{L})$ は Hilbert-Schmidt Independence Criterion (HSIC) と呼ばれるカーネルを用いた2変数間の独立性を測る基準の推定量です。

HSIC の気持ち

HSIC(a, b) は必ずゼロ以上の値をとり、またガウスカーネルのような稠密なカーネル関数 (universal kernel) を使っている場合、2つの変数が統計的に独立なときにゼロになり、その逆もなりたちます (ゼロであることと独立であることは同値)。また2つの変数の動きが連動していると大きな値を取ります。(a側が似ているとb側も似ていて, a側が似ていないときb側も似ていないと大きな値を取る)

やっていることの気持ちとしては「カーネルという類似度が入った空間でふたつの変数をみたとき、それぞれの連動している度合い(依存度合い)」を表している数値、といえます。

NOTE.2: 推定量

当たり前といえば当たり前ですが、先ほど定義した ${\rm HSIC} (u_k, y) = {\rm tr} (\tilde{K}^{(k)} \tilde{L})$ は HSIC の推定量であることに注意してください。実際の HSIC は真の分布がわかっていないと知ることができません。構造としては平均値の推定にデータの平均を使うのと一緒ですね。推定量が上手く機能しない (データが増えてもなかなか収束しないなど) と困りますがある種の収束をすることは保証されています。 *1

あてはまり・再掲

さてこの気持ちを念頭において、 HSIC であらわされた当てはまりの項をもう一度確認してみましょう。第一項は定数 ($y$ は動かないためです) ですからとりさってしまって$\alpha$ に関係する部分のみ再掲します。

$$ - \sum_{k=1}^{d} \alpha_k {\rm HSIC} (u_k, y) + \frac{1}{2} \sum_{k,l=1}^d \alpha_k \alpha_l {\rm HSIC} (u_k, u_l) $$

最初の項は特徴量の $d$ 次元目と目的変数 $y$ とがどれぐらい似通っているかを測っていることがわかります。 全体に負がかかっていますからこの部分を大きくするように、言い換えると $y$ に似ている次元ほど対応する係数 $\alpha_d$ も大きくなります。

また次の項は特徴量 $u, l$ 同士の類似度を見ていることがわかります。 この部分は小さくなるようになりますから、似ている冗長な変数の係数どうしの $\alpha$ は 0 に押しつぶされ、相互に似ていない特徴量の係数が相対的に大きくなることを意味しています。

結果として予測値 $y$ と動きが似ているもののうちで、互いに似ていない特徴量が選択されることになります。

Kernel の選択方法

入力に対してはガウスカーネルを使いますが、出力に対するカーネルは回帰問題と分類問題で使い分けを行っています。これは分類問題においてガウスカーネルを使うことは自然ではないから (実際ガウスカーネルを使った場合性能が悪化する at Figure4 )です。分類問題ではデルタカーネルを使うことが提案されています。

$$ L(y, y') = \begin{cases} 1/n_y\ &{\rm if}\ y= y' \\ 0\ &{\rm otherwise} \end{cases} $$

ここで $n_y$ はラベルが $y$ のデータの数です。これは予測値が特定のクラスになった時だけ値が存在するカーネルで、グラム行列でいえばone-hot へ変換したあとに列ごとに正規化しているような行列と表現できるかもしれません。

別の手法との関係性

論文中ではいくつかの手法が似ているものとして取り上げられていました。ここでは解釈が似ているものとして一番最初に提示されていた mRMR について述べていきます。

Minimum Redundancy Maximum Relevancy (mRMR)

HSIC Lasso を解釈する、のセクションで項毎の意味合いについて考えました。それは minimum redundancy maximum relevancy (mRMR) をベースとした特徴選択のアイディアに近いもので、名前の通り (特徴どうしの)冗長性は小さく・(目的変数との)関連性は大きくなるものが選ばれるような指標になっています。

mRMR は $m$ 個の特徴のみで構成した一部分の行列 $V \in \mathbb{R}^{m \times n }$ から

$$ {\rm mRMR}(V) = \frac{1}{m} \sum_{k=1}^m \widehat{{\rm MI}}(v_k, y) - \frac{1}{m^2} \sum_{k, l=1}^d \widehat{\rm MI}(v_k, v_l) $$

を計算して、この値がもっとも大きくなるような特徴集合 $V$ を選びます。ここで $\widehat{\rm MI}$ は経験相互情報量 (Empirical Mutual Information)*2 で, カーネル密度推定によって得られた確率密度関数 $\hat{p}_{x, y}$ を用いて以下のように計算されます

$$ \widehat{\rm MI}(x, y) = \int \int \hat{p}_{x, y} (x, y) \log \frac{ \hat{p}_{x, y} (x, y)} { \hat{p}_{x} (x) \hat{p}_{y} (y) } dx dy. $$

mRMR の第一項は目的変数と特徴との依存関係を、第二項は特徴量同士の依存関係を表していて、これは HSIC Lasso の解釈部分とにていることが解ると思います。また高速な実装可能な為高次元特徴量でも扱うことが可能です。

しかし mRMR は組み合わせごとに指標を計算しなくてはならない、という欠点があります。これにより、ナイーブにすべての組み合わせに対して計算を実行することは難しいので、貪欲方を使って要素を足したり・引いたりしつつ最適な組み合わせを探すことが実験的には使われますが、得られた解が局所的最適な特量の組み合わせになる可能性があります。*3

また mRMR ではカーネル密度推定によって密度関数を推定していますが、データ数が少ない時密度推定自体の信頼度が低くなり、上手く MI を推定できないことも指摘されています。たしかにそれはそうとう言う感じはします。

実験

3つのシナリオで実験が行われています。

人工データでの比較

まずは人工的に作成されたデータセットです。一つが加法性が成り立つ生成関数 (additive model) から作成された Data1、もうひとつが成り立っていない Data2 です。それぞれ 3 / 4 個の目的変数に関与する有効な変数と同時に、 256 / 1000 次元の無意味な特徴量も同時に加えています。

比較対象のアルゴリズムのなかに加法性を仮定しているもの (SpAM) があるため追加されているのかな?と想像しています。

f:id:dette:20210408194358p:plain
figure1. 人工データセットで正しく特徴が選べている割合を示したもの

実験結果は上記のとおりです。(a,b) ではデータの数を増やしていったときに、有効な変数をどのぐらいの割合選べたかを比較しています。これを見ると Data1/2 のどちらの場合も HSIC Lasso とそのバリエーションである NOCCO Lasso が上手く有効な特徴を選べていることがわかります。また (c) では他の手法と計算時間を比較していますがこちらを見ても比較的計算量の増加が緩やかであることがわかります。(d) では特徴量の次元数に応じて計算時間の比較をしていますが、傾きは変わらず大きなデータでも扱えることが見て取れます。

リアルデータでの比較

次に現実のデータ・セットを使って性能を比較します。まずは予測性能から。特徴選択に注目した予測性能の比較のため、実験は以下の3段階になっています。

  1. あるアルゴリズムをつかって有効な特徴量を k 個選択
  2. 選ばれた特徴量を使って機械学習モデルを学習
  3. hold-out されたデータに対する Accuracy を比較

2で学習する機械学習モデルにはガウスカーネルを用いた Kernel Logistic Regression を利用しています。

f:id:dette:20210408194450p:plain
figure2. 現実のデータでの性能比較. HSIC Lasso とその亜種の NOCCO がよさそう。

Figure2 を見ると画像系タスクでは提案手法が強く、それ以外のデータでも既存手法と同等かそれ以上の性能が発揮できていることがわかります。

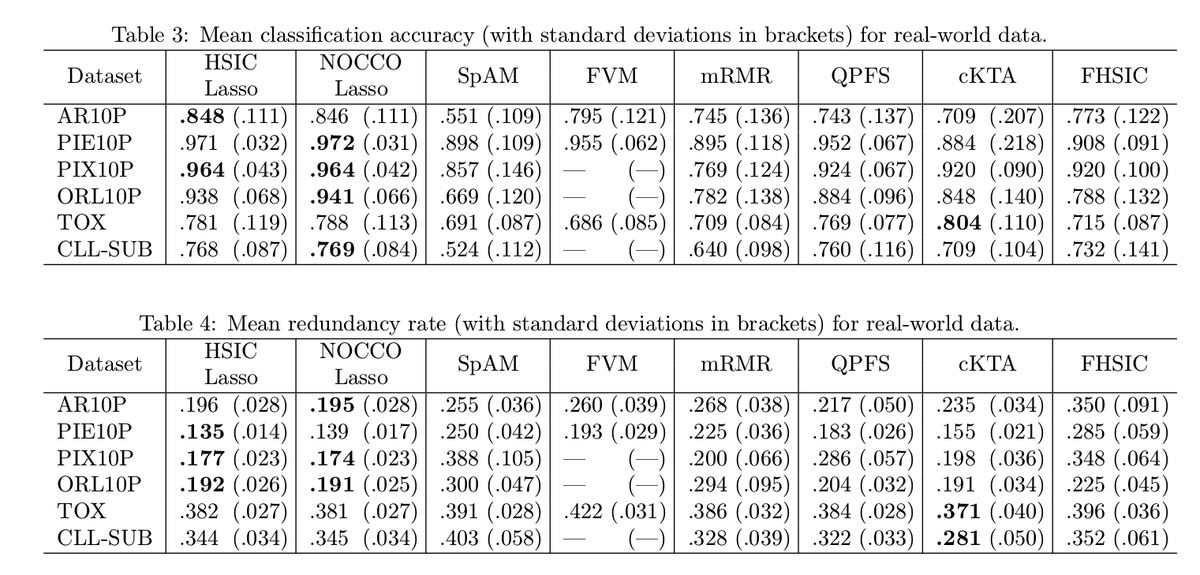
f:id:dette:20210408194536p:plain
table4. 冗長性に関する比較. 小さいほうが RAE の意味で相互作用の小さい特徴の組み合わせを選べていることを表す

Table4 では冗長性についても比較されています。冗長性は選ばれた特徴量同士の相関係数の平均値のことです。これを見ると提案手法の冗長性が低いことがわかります。比較手法のなかにある cKTA は (特徴選択ではない文脈で) 提案手法のようにグラム行列を使った目的関数を持っていて l1 正則化がないこと・Dualで解くこと以外が同じですので、提案手法は負けていますが HSIC をアルゴリズムのコアに持った手法が有効である、ということは言えそうです。

カーネルの選択での比較

HSIC Lasso はカーネル選択とカーネルを定めるハイパパラメータも問題設定を定めるパラメータの一つです。どのパラメータがセンシティブ、あるいはあまり気にしなくても良いパラメータなのかは気になるところです。

論文中では入力変数のガウスカーネルをスケールと、出力に対するカーネルの選び方 (Delta or Gaussian) で性能比較を行っています。

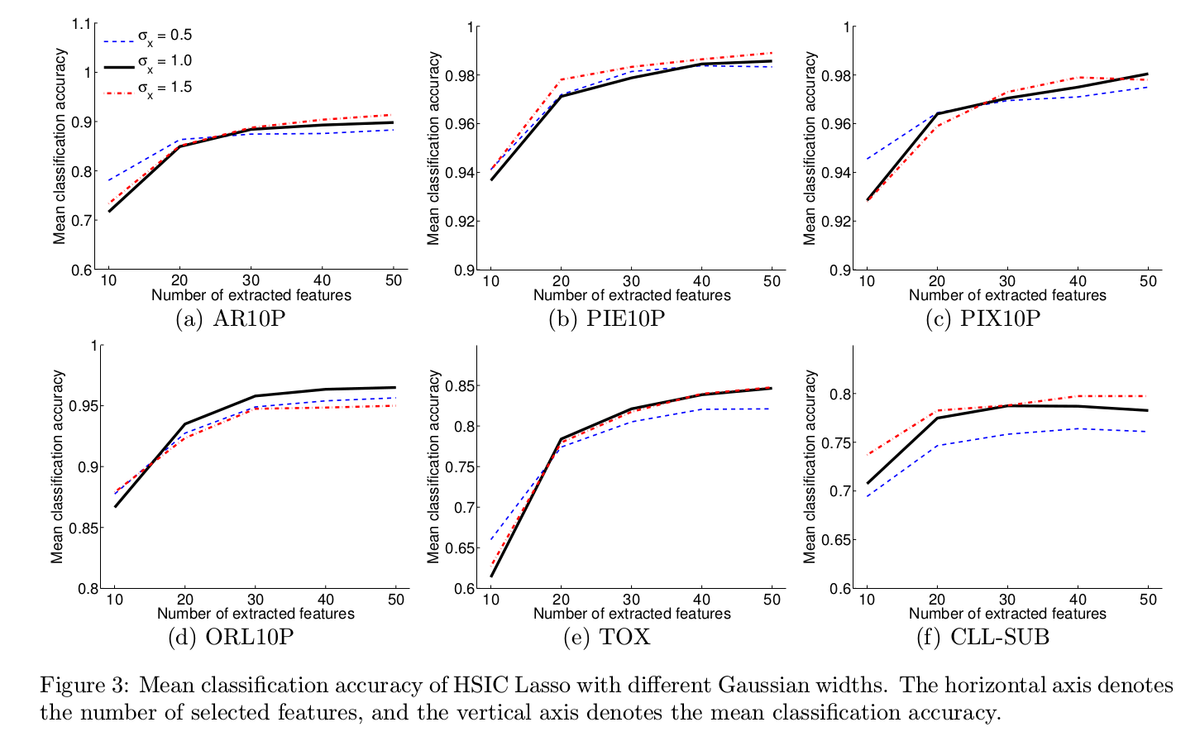
f:id:dette:20210408194704p:plain
Figure3. Gaussian Kernel のスケールでの比較。あまり差がない。

Figure3 は入力に対応するガウスカーネルのスケールごとの性能比較です。これを見るとあまり変化がなく、ガウスカーネルのスケールは大きな影響を与えないことがわかります。

f:id:dette:20210408194734p:plain
Figure4. 出力 $y$ に適用するカーネル種類での比較。Gaussian のスケールに比べるとかなり差があるように見える。

一方、Figure4 では出力のカーネルの種類での性能比較です。こちらを見ると Gaussian のとき大きく性能が悪化していることがわかり、入力出力でカーネルの種類を変えることが有効であることを示しています。また分類問題のラベルに対してガウスカーネルを考えることが不自然、という考えがある種正しいことの裏付けにもなっています。

高次元な問題での比較

最後に特徴量がとても多いデータ (データ数120 / 特徴量 31098) での比較を行っています。このデータはネズミの遺伝子がはいったデータです。タスクとしては特定の遺伝子 TRIM32 に近いものを探すというものです。*4遺伝子情報は実数ですので、解くのは回帰問題です。こちらも結果を見ると他の手法で得られた特徴に比べて良い性能を出していることがわかります。

個人的気になりポイント・感想

  • HSIC という基準をはじめて知った。世の中にはいろんな便利な道具があって考える人がいるんだなと改めておもった。
  • 上記に関連するが、HSIC の雰囲気がわかってない。あるデータとカーネルがあった時こうなるよ、という値の対応関係とかわかっているとより深く解釈ができて良さそうなので、実験してみたい。
  • HSIC Lasso を考えたひとは最初からこの定式化を思いついたのだろうか。最初は mRMR の形から逆算したのかな? (展開形式から L2 っぽく書き直した?) お気持ち気になる木。
  • 特徴選択アルゴリズムの比較で、学習させるモデルが線形でなかった場合どうなるのかが気になる。
    • 性能だけで言えば、論文で取り上げられていたカーネル Ridge より、勾配ブースティングなど一般に精度が高い (よりブラックボックス度の強めな) モデルはあるはず。そういうモデルで性能を比較すると、より色濃く差がでるのか、あるいは差が縮まるのかがきになるき

参考文献

*1:Measuring Statistical Dependence with Hilbert-Schmidt Norms Section3・4参照

*2:相互情報量は、変数Aの値を知った時に変数Bの不確実性がどのぐらい減るかを表したものと解釈することができる。モデルの予測の不確実性を調べる 敵対的サンプリング検出のための基準としての相互情報量 - Understanding Measures of Uncertainty for Adversarial Example Detection - nykergoto’s blog 見たいな文脈でも出てきたりする

*3:[memo]: HSIC Lasso は一度問題を解くと自然に特徴の重要度が得られますので、この点では HSIC が優っていると言えそう。

*4:ちょっと気になって元のデータにアクセスしてみたかったのですがオンラインで見られるところにはなさそうでした。残念。