FFT を使った時系列データ解析
今回は音声データやセンサーといった波形データの解析によく使われるFFTを、時系列のデータにつかって傾向の分析をやってみます、という話です。
FFTとは
FFT(高速フーリエ変換) はフーリエ変換 FT の高速版です。そのままですが。 めっちゃカジュアルに言えば、フーリエ変換(FT)は波形データからどの周期でどのぐらいの振れ幅を持っているかを抽出します。 工学の振動系とかだと、ノイズが混じった観測データから物体固有の振動を取り出したりとかに使ったり、まあ色々使われます。
この記事は FFT を使ってサンプルの波形の解析をやって、最後に日経平均の特性をちょっと見てみましょう、というのが主旨になっています。
FFT Module
python でフーリエ変換のモジュールというと有名なのは numpy.fft で基本的には
fftn: 波形空間からフーリエ変換した強度空間への射影を行う関数ifftn: フーリエ変換された強度から元の波形空間へ戻す関数fftfreq: フーリエ変換した強度関数がどの周波数に対応しているかの周波数を計算する関数
の3つを使うことが多い印象です。 scipy のほうが早いらしいので変換がボトルネックになるような巨大データを扱うときは numpy からそちらに移行することも考えてみてください。
それぞれのドキュメントは https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.fft.html から見れます。
実際にやってみる
まずは下準備から
import numpy as np from numpy.fft import fftn, ifftn, fftfreq import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import os output_dir = './fft_vis' os.makedirs(output_dir, exist_ok=True) def save_fig(fig, name): p = os.path.join(output_dir, name) print(f'save to {p}') fig.tight_layout() fig.savefig(p, dpi=120)
サンプルデータの準備
始めにサンプルの周期的な関数を使って、動作を確認してみます。
仮に周期が 3 の波にランダムなノイズが乗っているものを考えてみます。
周期が 3 の波を作るためには, 適当な x に対して, $1 / 3 \times 2 \pi * x$ を計算すればOKです。
今回は周期が 3 と 0.5 の波を足し合わせたものにガウスノイズをちょっと加えたものを分析対象にします。強度はそれぞれ 1, 0.7, 0.3 としています。
# データの総数 n_samples = 300 # 単位時間あたりに, いくつのデータ点が存在しているか. sampling_rate = 10 # サンプルデータ作成のために, 1 / sampling_rate ごとの等間隔な x を用意 x = np.arange(n_samples) / sampling_rate # 作成した x を入力として, 周期 3 と 0.5 の波形 (+ノイズ) を足し合わせる. y = np.sin(1 / 3 * 2 * np.pi * x) + .7 * np.sin(2 * 2 * np.pi * x) + .3 * np.random.normal(size=n_samples) # あとでの遊びのために 10 のところでわざとピークをつける y += np.where(x == 10, 5, 0)
fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, y) ax.set_title('サンプル波形')

実際にフーリエ変換してみます。
フーリエ変換する関数は fftn です。普通に使うには波形データを代入すればOKです。
出力は周波数ごとの強度になっているので、どの周波数に対応するか計算する必要があります。
これを助けてくれるのが fftfreq です。波形データの総数とサンプリングレート (Hz) を d に代入します。
d は一秒間のデータ数の逆数であることに注意して下さい。
z = fftn(y)
freq = fftfreq(n_samples, d=1 / sampling_rate)
FFT の出力のみかた
FFT は元の空間の出力値から, 各周波数ごとの強度に変換します。
一般に横軸に周波数もしくは周期をとり、縦軸にその周波数での強度を取ることが多いです。
強度各周波数ごとに出力されますが, どのぐらい綺麗な sin からずれているかの位相遅れ成分が含まれている為, 複素数で表現されています。そのため強度として表示する際には絶対値を取ることが多いです。またその際 logscale にして表示するのが一般的です。(マグニチュードとかと同じ)
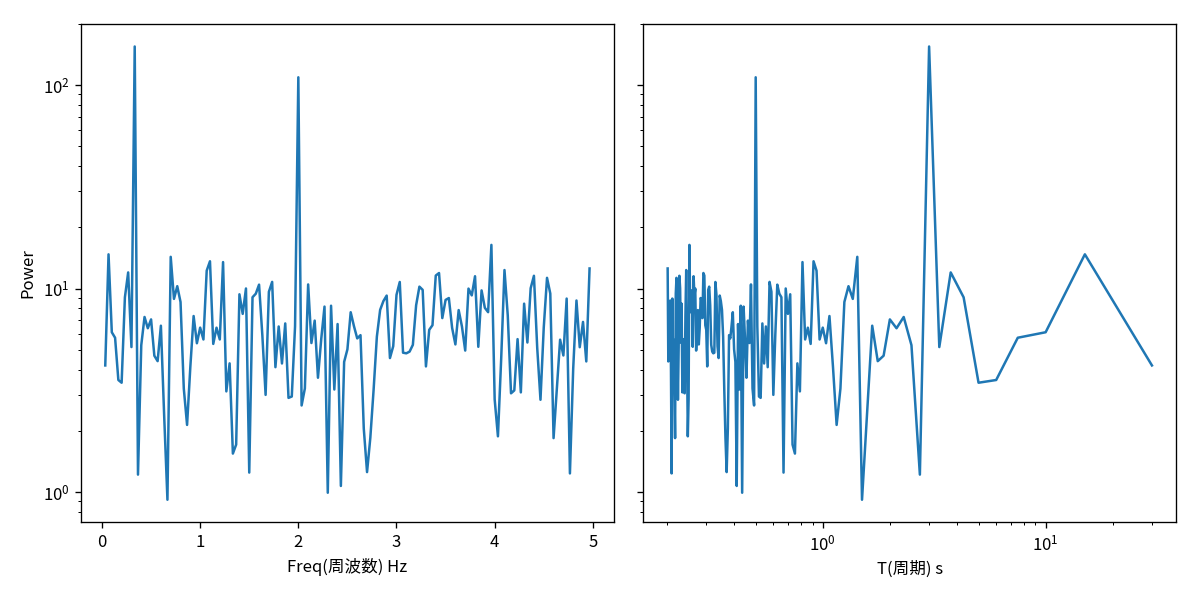
# ノリのような表示 # plt.plot(freq, abs(z)) #plt.yscale('log') # 適当にやるとマイナスの周波数も表示される. +-で値は同じ(y軸対象)なのでプラス部分だけ可視化すれば十分 # 真面目に fig, axes = plt.subplots(figsize=(10, 5), ncols=2, sharey=True) ax = axes[0] ax.plot(freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('Freq(周波数) Hz') ax.set_ylabel('Power') # 周波数 f → 周期 T に直して表示する # 周期は fT = 1 を満たすので単に逆数にすれば良い ax = axes[1] ax.plot(1 / freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('T(周期) s') ax.set_xscale('log') save_fig(fig, name='sample_wave_fft.png')
fft_pow_df = pd.DataFrame([1 / freq[1:int(n_samples / 2)], np.log10(abs(z[1:int(n_samples / 2)]))], index=['T', 'log10_power']).T fft_pow_df.sort_values('log10_power', ascending=False).head(10)
| T | log10_power | |
|---|---|---|
| 9 | 3.000000 | 2.189058 |
| 59 | 0.500000 | 2.037770 |
| 118 | 0.252101 | 1.214322 |
| 1 | 15.000000 | 1.167947 |
| 20 | 1.428571 | 1.155673 |
| 32 | 0.909091 | 1.133798 |
| 36 | 0.810811 | 1.129822 |
| 148 | 0.201342 | 1.098518 |
| 122 | 0.243902 | 1.090790 |
| 31 | 0.937500 | 1.087703 |
np.log10(1 / 0.7)
0.15490195998574316
考察
ちゃんと周期が 3 と 0.5 のところにピークが有ることがわかります。
ログスケールでの強度の差分は大体 0.15 で作成した時の強度の比の log10 の値 log_10(1/.07) とほぼ一致していることも確認出来ます。
IFFT (逆フーリエ変換)
フーリエ空間の波形強度から元の波形空間へ戻すこともできます。べんりですね。これを逆フーリエ変換(Inverse FT: IFT) といいそれを高速にするので IFFT (Inverse Fast FT) です。 フーリエ変換したあとの情報すべてを使うと、完全に元通りにすることが出来ます。
この時戻した値の実数値成分
realをつかうのをお忘れなく。ifftの返り値は数値計算の誤差で、微妙に複素数成分が含まれた値が帰ってくるので実数値だけを取り出すようにします。(ノルムにしてもいい気がするけれどまあほぼ誤差なので気にしなくても良い?)
fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(ifftn(z).real, label='IFFT') ax.plot(y, label='Original') ax.legend() save_fig(fig, name='sample_wave__ifft.png')

Low Pass Filter
先の IFFT では変換した z をすべて使って元に戻しました。ですのでまったく同じ波形になりました。
ここで, Low な frequency の周波数成分のみを使って IFFT しましょうというのが Low Pass Filter です。
要するに FFT した結果のうち, 周波数が一定以下のゆったりとした波形のみをつかって(反対に言うと高周波の凄い急な振動は消して), もとの波形空間に戻すという方法です。
これをすることで波形全体の中から細かい揺れの成分を消すことができるので、波形全体の大まかな傾向をつかむことが出来ます。
一般にセンサーのノイズとかはホワイトノイズ (np.random.norm) になるためこの影響を小さくして、センサーでとりたい対象本来の波形を抽出するのに使われたりします。
全体の傾向を取ったような関数になるので移動平均と似たなものになる。短期的な変動が消えるので簡易的な異常値検知には使えるかもしれません。
*1
ためしに先ほどわざと混入させた x=10 の場所での異常値を検出してみましょう。
# 2以下の周期を無視する様な lowpass threshold_period = 2 threshold_freq = 1 / threshold_period z_lowpass = np.where(abs(freq) > threshold_freq, 0, z) y_lowpass = ifftn(z_lowpass).real fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, y, '-', label='Original', alpha=.5) ax.plot(x, y_lowpass, label='LowPass') ax.set_title('Low Pass Filter') ax.legend() save_fig(fig, name='sample_wave__lowpass.png')

異常値が見たければ元の値と lowpass の差分を見れば良いので適当に引いて絶対値にします。
diff = abs(y_lowpass - y) fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, diff) ax.set_ylabel('diff btw lowpass and original') save_fig(fig, name='sample_wave__diff_lowpass.png')

print(x[np.argmax(diff)])
10.0
ちゃんと 10 のとこに一番異常な点が有ることがだせました。嬉しい:D
発展: 日経平均の分析
以上で試したことを日経平均の分析に適用してみましょう。 データは [https://indexes.nikkei.co.jp] さんよりお借りした日経平均株価をつかいます。
url = 'https://indexes.nikkei.co.jp/nkave/historical/nikkei_stock_average_daily_jp.csv' nikkei_df = pd.read_csv(url, encoding='shift_jis')
# 最終行は著作権に関する情報なので、分析には使わないように。 nikkei_df = nikkei_df.iloc[:-1, :]
nikkei_df.head()
| データ日付 | 終値 | 始値 | 高値 | 安値 | |
|---|---|---|---|---|---|
| 0 | 2016/01/04 | 18450.98 | 18818.58 | 18951.12 | 18394.43 |
| 1 | 2016/01/05 | 18374.00 | 18398.76 | 18547.38 | 18327.52 |
| 2 | 2016/01/06 | 18191.32 | 18410.57 | 18469.38 | 18064.30 |
| 3 | 2016/01/07 | 17767.34 | 18139.77 | 18172.04 | 17767.34 |
| 4 | 2016/01/08 | 17697.96 | 17562.23 | 17975.31 | 17509.64 |
一旦可視化してみましょう
nikkei_df['データ日付'] = pd.to_datetime(nikkei_df['データ日付']) nikkei_df = nikkei_df.set_index('データ日付') fig, ax = plt.subplots(figsize=(len(nikkei_df) * .02, 5)) nikkei_df.plot(ax=ax)
これを見ると若干 FFT の仮定である定常的な波 (一定周期で同じ波形を繰り返す) が成り立っているか微妙ですね… 特に始めと終わりの値が結構ずれているので端点で相当無理が生じそうです。
FFTでは波形に周期があることが仮定されています。ですので今回の日経平均の用に入力データの端点が揃っていない場合、その仮定が成り立たず正直かなり良くありません。
この補正をするのが窓関数で hamming 窓などが有名です。(窓関数を使う理由に関しては https://www.logical-arts.jp/archives/124 がとても詳しいです。)
今回はローパスフィルタを作りたいというのもあるので一旦窓の適用はせずに分析しますが以下の分析結果は眉唾で聞いて下さい
系列はほとんどすべて同じなので終値を使うことにします。
y = nikkei_df['終値'].values # 窓関数使うときは window を作って掛け算. # y = y - np.mean(y) # window = np.hamming(len(y)) # y = y * window x = nikkei_df.index
n = len(y) z = fftn(y) # 単位時間は日でサンプリングレートも1なので `d=1` を指定 freq = fftfreq(n, d=1)
fig, axes = plt.subplots(figsize=(10, 5), ncols=2, sharey=True) ax = axes[0] ax.plot(freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('Freq(周波数) Hz') ax.set_ylabel('Power') ax = axes[1] ax.plot(1 / freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('T(周期) s') ax.set_xscale('log') save_fig(fig, name='nikkei_fft.png')

nikkei_pow_df = pd.DataFrame([1 / freq[1:int(n_samples / 2)], np.log10(abs(z[1:int(n_samples / 2)]))], index=['T', 'log10_power']).T nikkei_pow_df.sort_values('log10_power', ascending=False).head(10)
| T | log10_power | |
|---|---|---|
| 0 | 860.000000 | 6.098400 |
| 1 | 430.000000 | 5.461296 |
| 2 | 286.666667 | 5.456172 |
| 4 | 172.000000 | 5.416735 |
| 5 | 143.333333 | 5.220405 |
| 6 | 122.857143 | 5.212416 |
| 7 | 107.500000 | 5.128081 |
| 3 | 215.000000 | 5.068687 |
| 9 | 86.000000 | 5.033504 |
| 17 | 47.777778 | 4.920812 |
周波数成分からわかること
- 長周期の成分が大きそうです。定期的な繰り返しというよりは大きく平均値が変わるような変動をしているといえます。
正直その程度はぱっと見れば誰でもわかりますがそれを定量的に評価できているのは良い点かもしれません。 - 意外と一週間とか一ヶ月の周期は出てこない。月曜日だから買う!とかいう人は居ないんですね(当たり前)
ついでに Low Pass Filter もやってみましょう
# 30日以下の周期を無視する様な lowpass threshold_period = 30 threshold_freq = 1 / threshold_period z_lowpass = np.where(abs(freq) > threshold_freq, 0, z) y_lowpass = ifftn(z_lowpass).real fig, axes = plt.subplots(figsize=(10, 8), nrows=2, sharex=True) ax = axes[0] ax.plot(x, y, '-', label='Original', alpha=.5) ax.plot(x, y_lowpass, label='LowPass') ax.set_title('Low Pass Filter') ax.legend() ax.set_ylabel('日経平均終値') diff = y_lowpass - y ax = axes[1] ax.plot(x, abs(diff)) ax.set_ylabel('LowPassFilterとの差分') ax.set_xlabel('日付') fig.tight_layout() save_fig(fig, name='nikkei_diff_lowpass_and_original.png')

やはり周期性が成り立っていないものに対して端の値を合わせようとしているために 2016-01 と 2017-07 の値は差分が大きいです。やっぱり日経平均に適用するのはむりがあったかも…反省…
このような端点も見るためには、局所的な情報を使うスペクトログラムとか使う必要がありそうです。(スペクトログラムは局所的な幅 (window) の中で FFT をいくつもやるようなイメージです。なので波形全体で周期性がなくてもその場その場での傾向を可視化出来ます。やってからこれはFFTのお仕事ではないなと)
端を除外して, ぱっと目立つのは 2016年にひとつ有る大きな暴落と2019年になるあたりでの急上昇と急降下でしょうか。
_df = pd.DataFrame([diff, x], index=['diff', 'date']).T.sort_values('diff', ascending=False)
_df.head(10)
| diff | date | |
|---|---|---|
| 27 | 1345.16 | 2016-02-12 00:00:00 |
| 209 | 1199.49 | 2016-11-09 00:00:00 |
| 733 | 1155.33 | 2018-12-25 00:00:00 |
| 12 | 1044.84 | 2016-01-21 00:00:00 |
| 5 | 998.391 | 2016-01-12 00:00:00 |
| 0 | 981.503 | 2016-01-04 00:00:00 |
| 3 | 910.682 | 2016-01-07 00:00:00 |
| 734 | 907.997 | 2018-12-26 00:00:00 |
| 514 | 859.389 | 2018-02-06 00:00:00 |
| 1 | 802.091 | 2016-01-05 00:00:00 |
_df.tail(10)
| diff | date | |
|---|---|---|
| 854 | -866.97 | 2019-07-01 00:00:00 |
| 18 | -922.626 | 2016-01-29 00:00:00 |
| 76 | -1031.42 | 2016-04-22 00:00:00 |
| 855 | -1099.33 | 2019-07-02 00:00:00 |
| 856 | -1208 | 2019-07-03 00:00:00 |
| 20 | -1247.26 | 2016-02-02 00:00:00 |
| 19 | -1318.26 | 2016-02-01 00:00:00 |
| 857 | -1510.47 | 2019-07-04 00:00:00 |
| 858 | -1802.45 | 2019-07-05 00:00:00 |
| 859 | -1844.78 | 2019-07-08 00:00:00 |
まとめ
波形データの特性を見るのに使われる FFT の使い方をざっくり紹介しました。 使ったデータに定常性が対してなかったこともあり、今回はあまり良い傾向の分析は出来ず残念でしたが、系列データの特性を数値的に表現できる便利ツールなので、EDAとかに使うと説得力があってよいかなーと思います。
*1:もちろんこれは相当不真面目な異常検知です。真面目にやるときは系列データの生成モデルなりを仮定して、生成される確率が小さい時にアラート、などやる必要があります。
