PRML 10章の変分ベイズ法の実装

線形回帰に対する変分法を用いた計算について実装してみました。

コードは以下から
github.com

変分ベイズではまず、隠れ変数も含めた完全データに対して同時分布を定義します。その後隠れ変数の分布が複数の関数の積として近似して表すことができる、という仮定を導入します。

このことによって、完全データに対する同時分布を、目的の隠れ変数以外の事後分布で周辺化したものが、新しい近似事後分布となり、それをすべての隠れ変数に対して繰り返して計算していくことにより、より尤度の高い隠れ変数の事後分布を計算していく、という手法です。

今回は次のグラフィカルモデルで表すことができる確率モデルに対して、変分ベイズ方を適用します。

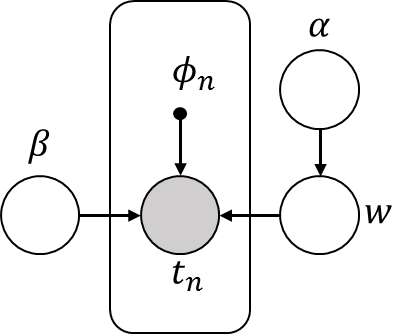
PRML10.3と似ていますが、実際のラベルデータが生成される際の精度パラメータβに対しても分布を定義している部分が異なっています。βに分布をもたせるとどのぐらい変化があるのかということを確かめたかったので、βにも分布をもたせました。

データとしては正しいsin関数にsigma=.5のガウスノイズを付加したデータを用います。

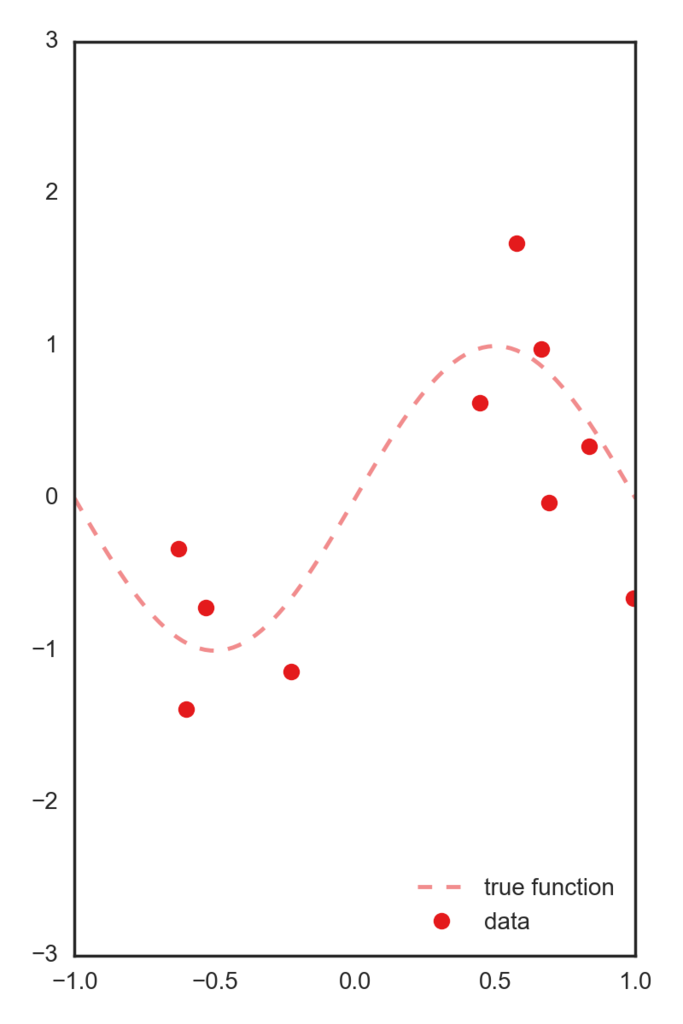
この一次元特徴を、[-1~1]を５個に分割した中心を持つガウス基底によって５次元空間に写像したデータを特徴量として用います。 以下コードです。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

np.random.seed(71)


def t_func(x):
    """正解ラベルを作る関数
    x: numpy array.
    return t: target array. numpy.array like.
    """
    t = np.sin(x * np.pi)
    # t = np.where(x > 0, 1, -1)
    return t


def plot_target_function(x, ax=None, color="default"):
    """target関数（ノイズなし）をプロットします
    """
    if ax is None:
        ax = plt.subplot(111)
    if color is "default":
        color = "C0"
    ax.plot(x, t_func(x), "--", label="true function", color=color, alpha=.5)
    return ax


def phi_poly(x):
    dims = 3
    return [x ** i for i in range(0, dims + 1)]


def phi_gauss(x):
    bases = np.linspace(-1, 1, 5)
    return [np.exp(- (x - b) ** 2. * 10.) for b in bases]


def qw(alpha, phi, t, beta):
    """
    wの事後分布を計算します。
    変分事後分布はガウス分布なので決定すべきパラメータは平均と分散です
    w ~ N(w| m, S)
    return ガウス分布のパラメータ m, S
    """
    S = beta * phi.T.dot(phi) + alpha * np.eye(phi.shape[1])
    S = np.linalg.inv(S)
    m = beta * S.dot(phi.T).dot(t)
    return m, S


def qbeta(mn, Sn, t, Phi, N, c0, d0):
    """
    betaの変分事後分布を決めるcn,dnを計算します
    変分事後分布はガンマ分布なので決定すべきパラメータは2つです
    beta ~ Gamma(beta | a, b)
    return ガンマ分布のパラメータ a,b
    """
    cn = c0 + .5 * N
    dn = d0 + .5 * (np.linalg.norm(t - Phi.dot(mn)) **
                    2. + np.trace(Phi.T.dot(Phi).dot(Sn)))
    return cn, dn


def qalpha(w2, a0, b0, m):
    """
    alphaの変分事後分布を計算します。
    変分事後分布はガンマ分布ですから決定すべきパラメータは2つです
    alpha ~ Gamma(alpha | a, b)
    return a, b
    """
    a = a0 + m / 2.
    b = b0 + 1 / 2. * w2
    return a, b


def fit(phi_func, x, update_beta=False):
    xx = np.linspace(-2, 2., 100)
    if phi_func == "gauss":
        phi_func = phi_gauss
    elif phi_func == "poly":
        phi_func == phi_poly
    else:
        if type(phi_func) == "function":
            pass
        else:
            raise Exception("invalid phi_func")
    Phi = np.array([phi_func(xi) for xi in x])
    Phi_xx = np.array([phi_func(xi) for xi in xx])

    # 変分事後分布の初期値
    N, m = Phi.shape
    mn = np.zeros(shape=(Phi.shape[1],))
    Sn = np.eye(len(mn))
    beta = 10.
    alpha = .1
    a0, b0 = 1, 1
    c0, d0 = 1, 1

    pred_color = "C1"

    freq = 2
    n_iter = 3 * freq
    n_fig = int(n_iter / freq)

    fig = plt.figure(figsize=(3 * n_fig, 4))
    data_iter = []
    data_iter.append([alpha, beta])

    for i in range(n_iter):
        print("alpha:{alpha:.3g} beta:{beta:.3g}".format(**locals()))

        mn, Sn = qw(alpha, Phi, t, beta)
        w2 = np.linalg.norm(mn) ** 2. + np.trace(Sn)
        a, b = qalpha(w2, a0, b0, m)
        c, d = qbeta(mn, Sn, t, Phi, N, c0, d0)

        alpha = a / b

        if update_beta:
            # betaが更新される
            beta = c / d

        data_iter.append([alpha, beta])

        if i % freq == 0:
            k = int(i / freq) + 1
            ax_i = fig.add_subplot(1, n_fig, k)
            plot_target_function(xx, ax=ax_i)
            ax_i.plot(x, t, "o", label="data", alpha=.8)

            m_line = Phi_xx.dot(mn)
            sigma = (1. / beta + np.diag(Phi_xx.dot(Sn).dot(Phi_xx.T))) ** .5
            ax_i.plot(xx, m_line, "-", label="predict-line", color=pred_color)
            ax_i.fill_between(xx, m_line + sigma, m_line - sigma, label="Predict 1 sigma", alpha=.2, color=pred_color)
            ax_i.set_title(
                "n_iter:{i} alpha:{alpha:.3g} beta:{beta:.3g}".format(**locals()))
            ax_i.set_ylim(-2, 2)
            ax_i.set_xlim(-1.5, 1.5)
        if i == 0:
            ax_i.legend(loc=4)

    fig.tight_layout()
    return fig, data_iter

まずはβを更新せずハイパーパラメータとして与えて、変分ベイズを適用します。(β=10で固定)
一番左が初期値での最尤推定値となっていて、右に行くほど変分ベイズ法によって更新された分布情報に基づいた予測値になっています。今回与えたβが、実際の精度パラメータよりも大きな値を取っているために、データ点に過剰にフィットしていることが伺えます。

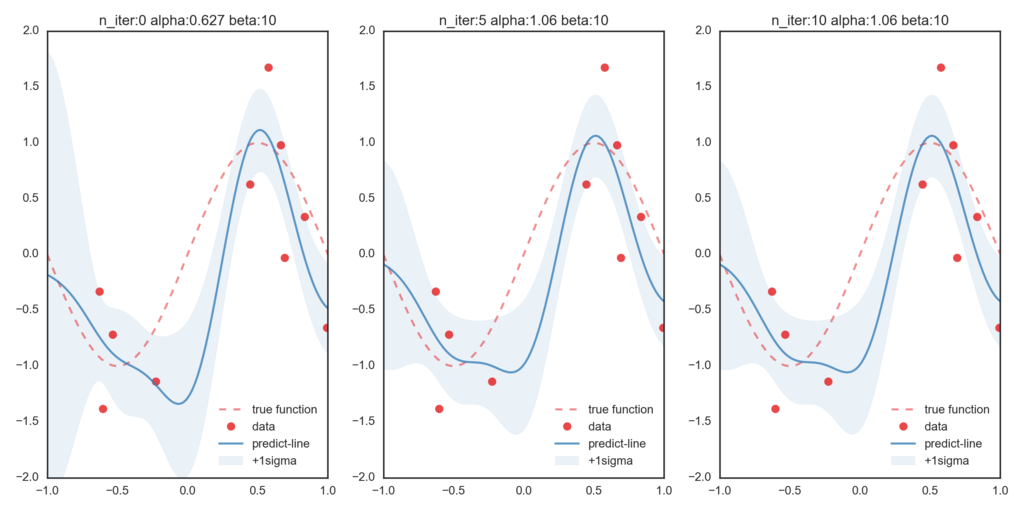
つぎにβを変分ベイズ法で更新したのが次のグラフです。比べてみると、βが更新されることによって正しい関数に近づいていることが確認できます。