RAdam: Adam の学習係数の分散を考えたOptimizerの論文紹介
表題の通り噂の最適化手法 RAdam の論文 On the Variance of the Adaptive Learning Rate and Beyond を読んだので, そのまとめです!!
概要
一言でいうと「今までヒューリスティックに行っていた Adam 学習開始時の LR 調整を自動化できるような枠組みをつくったよ」ということになると思います.
考える問題
この論文で, 考えていくのは機械学習のように多数のデータから成る目的関数を最小化するような問題です. 特にニューラルネットワークの学習では勾配法, 特に SGD (確率的勾配降下法) と呼ばれる方法を用いることが一般的です.
SGD には様々な adaptive バリエーションがあります.この adaptive とは問題の特性を生かして, SGD を早くするような工夫を指しています.
一般的な形式
一般的な adaptive と呼ばれる SGD は, 方向を決める $\phi$ とそれを補正する係数である $\psi$ を用いて記述することができます.
例えば adam の場合は勾配には勾配の指数加重平均を, 補正係数には勾配の要素ごとの二乗の指数加重平均を用います.
具体的に書き下すと第 $t$ ステップでの更新は, $t$ ステップで得られたサンプルに対する勾配 $g_t$ から
$$ m_t = \frac{(1 - \beta_1) \sum_{i=1}^t \beta_1^{t-i} g_i}{1 - \beta_1^t} \\ V_t = \frac{(1 - \beta_2) \sum_{i=1}^t \beta_2^{t-i} g_i^2}{1 - \beta_2^t} $$
とおいたときに更新したいパラメータ $x_t$ を
$$ x_{t+1} = x_t - \alpha_t \frac{1}{\sqrt{V_t}}m_t $$
として更新を行っていきます. ここで $\beta_1, \beta_2 \in [0, 1]$ は勾配/補正係数の指数加重平均のハイパーパラメータで $\alpha_t \in {\mathbb R}$ は学習係数 (Learning Rate) です。 また $g_i^2$ は成分ごとの二乗を表しています. 即ち $(g_i^2)_j = (g_i)_j^2$ です.
このあたりは僕のスライドになってしまいますが https://speakerdeck.com/nyk510/que-lu-de-gou-pei-fa-falsehanasi?slide=7 あたりを見て雰囲気を掴んでいただけると, あとの話がスムーズに進むかなと思います.
この論文では主に $V_t$ について取り扱いますが, ルートをとって逆数を撮った形式を標準形 $\psi$ として扱います.すなわち
$$ \psi_t = \frac{1}{\sqrt{V_t}} = \sqrt{\frac{1 - \beta_2^t}{(1 - \beta_2) \sum_{i=1}^t \beta_2^{t-i} g_i^2}} $$
を以下では扱います.
SGD の warm start
SGD では学習の初期に小さな LR を使って更新を行い, ある一定のステップが立ったのちに通常の LR を使って SGD を使う, という戦略が取られることがあります. これを warm start といい, adam やその他の adaptive な学習法でも有効であることが確認されています.
warm start が有効な理由
ではなぜ warm start が有効なのでしょうか. 例として Adam でステップ $t=1$ の時を考えてみます.その時補正係数は
$$ \psi_1 = \sqrt{\frac{1}{g_t^2}} $$
となります.このとき仮定として勾配 $g_t$ が正規分布 $N(0,\sigma^2)$ から生成されているとすると $\frac{1}{g_t^2}$ は $\sigma^2$ でスケール化された自由度1のカイ二乗分布の逆数となります.(これを論文中では Scale-inv-$\chi^2 (1, \frac{1}{\sigma^2})$ と表記しています)
このとき $\psi$ の分散は
$$ Var[\psi] \propto \int_{0}^{\infty} x e^{-x} dx = \infty $$
となり発散します.この例で見たようにステップ $t$ が小さいときには補正項の分散は bound されません. したがって補正係数がとても大きい値を取る場合があり挙動が不安定になってしまいます.
論文中でも Figure2 で初期の step の更新で重みの分布が崩壊して学習が上手く進まなくなってしまう様子が可視化されています。

このような不安定性を抱えているため何らかの手段を講じる必要がありますが、その一つの手段が warm start です. warm start では $t$ が小さい領域では lr を小さくするため, 補正係数で bound されない分の上限を lr が変わりに行ってくれます.
このため安定した学習が可能になります. またステップが増えていくと $\psi$ の分散は bound されてくるので lr での bound は初期のステップの範囲だけでOKなこともわかります.
Adam の補正係数の分散
step $t$ が小さい時を考えます.このとき指数加重平均を行う際の重みの差分は $1-\beta_2^t$ 以内に収まります. $\beta_2$ は普通 0.99 程度なので $t$ が小さいときに差分が小さいことがわかります. このことから初期ステップでの指数加重平均は, おおよそ過去の勾配の平均をとったので問題がない, ということがわかります.すなわち
$$ \frac{(1-\beta_2)\sum_{i=1}^t\beta_{2}^{t-i} g_i^2}{1-\beta_2^t} \sim \frac{\sum_{i=1}^t g_i^2 }{t} $$
とみなせます.これを $\psi$ に当てはめると自由度 $t$ の Scaled inverse $\chi^2 (t, 1/\sigma^2)$ となります.
ではこの分布に従う $\psi$ の分散はどの様になるでしょうか? これを述べているのが Theorem.1 で結論を言うと 自由度を $\rho$ としたとき $\rho$ が増えるに従って分散は単調減少します. (正確には任意の $\rho > 4$ に対して上記が成立します)
これによってステップが増えていけば分散は縮小することがある程度保証されました. ではこの $\rho$ をどのように推定するのか? が次の話題になります.
自由度 $\rho$ の推定
$\rho$ を推定する際に使うのが Simple Moving Average (SMA) という考え方です.これは直近の $f(t,\beta_2) \in {\mathbb N}$ のステップで指数平滑移動平均を近似する, というものです.すなわち
$$ p\left( \frac{(1-\beta_2)\sum_{i=1}^t\beta_{2}^{t-i} g_i^2}{1-\beta_2^t} \right) \sim p \left( \frac{\sum_{i=1}^{f(t,\beta_2)} g_i^2 }{f(t,\beta_2)} \right) $$
を満たす, ということです.これを先の議論と合わせて考えると自由度 $\rho$ は $f(t,\beta_2)$ とみなせます.
この $g_i$ に対して $g_i = (t + 1 -i)$ であっても成り立ってほしい!ということで単に代入してやると
$$ p \left( \frac{(1-\beta_2)\sum_{i=1}^t\beta_{2}^{t-i} (t + 1 -i)}{1-\beta_2^t} \right) \sim p \left( \frac{\sum_{i=1}^{f(t,\beta_2)} (t + 1 -i) }{f(t,\beta_2)} \right) $$
を満たしている必要があるということになります. これを解くと*1
$$ f(t, \beta_2) = \frac{2}{1-\beta_2} - 1 - \frac{2t\beta_2^t}{1 - \beta_2^t} $$
を得ます.これを見ると $t \to \infty$ のとき $\rho_{t} \to \frac{2}{1 - \beta_2} - 1$ であることがわかります.(この値を $\rho_{\infty}$ とおきましょう) また $ \frac{2t\beta_2^t}{1 - \beta_2} > 0$ であることを考慮すると, $\rho_t < \rho_{\infty}$ であることもわかります.
$\psi$ の分散推定
では次に $\psi$ の分散がどの様になるのか考えていきます. 煩雑になるので飛ばしましたが Theorem.1 で分散を厳密に計算することができ, そのオーダーは $Var[\psi] = O(\frac{1}{\rho_t})$ であることがわかっています.(単に式変形するだけです) これと Theorem.1 の主張である「$\rho$ が大きいとき分散は小さい」を組み合わせると, 分散の最小値は $t \to \infty$ のとき, すなわち
$$ \min_{\rho_t} Var[\psi] = Var[\psi] |_{\rho_t = \rho_\infty} $$
であることがわかります(この最小値を $C_{var}$ とおきます.). すなわち $\rho_\infty$は計算可能ですから分散の最小値は見積もれる, ということです.
ここで, 学習が進むにつれて補正係数 $\psi$ のオーダーは変化しないことが望ましいことを思い出してください. これは補正係数が変わってしまうと, 最適な LR の値もかわってしまうためです.
したがって各ステップでの補正係数は, $C_{var}$ 程度の大きさになるようになってほしい, ということです. すなわちもともとの adam などの補正係数 $\psi_t$ に対して修正用の係数を $r_t \in {\mathbb R}$ かけて
$$ Var[r_t \psi] = C_{var} $$
が満たされていてほしいです.すなわち
$$ r_t = \sqrt{\frac{C_{var}}{Var[\psi]}} $$
を満たすように $r_t$ を選べば良いことがわかります. ではあとは計算するだけ, ですがこの係数を見積もるためには $Var[\psi]$ を知っている必要があります. これは解析的に計算することが困難なので ${\mathbb E}[\psi^2]$ の周りで Taylor 展開をした一次の部分を使ってやると
$$ Var[\psi] \sim \frac{\rho_t}{2(\rho_t - 2)(\rho_t - 4)\sigma^2} $$
を得ることができます.これと $\rho > 4$ のとき $Var[\psi]$ が単調減少であることを考慮すると $\rho > 4$ の範囲において
$$ r_t = \sqrt{\frac{(\rho_t - 4)(\rho_t - 2) \rho_\infty}{(\rho_\infty - 4)(\rho_\infty - 2) \rho_t}} $$
を設定することが良いことがわかります.
以上を記述したのが Algorithm.2 になっています.

はじめ各ステップで $\rho_t$ を計算します.この $\rho_t$ が大きいときは $Var[\psi]$ が小さいことを示していますから, Adam のような補正をかけることが正当です. 具体的には $\rho > 4$ の条件に合うかどうかを調べて当てはまった場合上記の補正を入れた勾配+補正項で更新します.
そうでない $Var[\psi]$ が大きいときには更新が十分に行われていないと判断して補正項を使わずに勾配のみを使って momentum で更新を行います.
ここで $\beta_2$ が小さいとき、具体的には0.6以下のときには $\rho_t $ がつねに4以下になる、ということに注意してください。
要するに $\beta_2$ があまりに小さすぎると $Var[\psi]$ は常に大きな値を取り続けると想定されるため Adam のような adaptive な更新を行うことは不適切 と判断される、ということです。この場合ずっと momentum のみの更新が行われます.
実験と考察
はじめに pure な Adam と SGD との比較を行っています.

この結果を見ると pure Adam にはどちらの条件でも勝っていることがわかります. *2
上記の実験は最も良いものを tuning した結果でしたが実際に実験する際にはどのようなパラメータでも学習がうまく進むことが望ましいですよね. それを調べるべくいちばん大事なパラメータ LR に対して学習がどのように変化するかが次のグラフです.
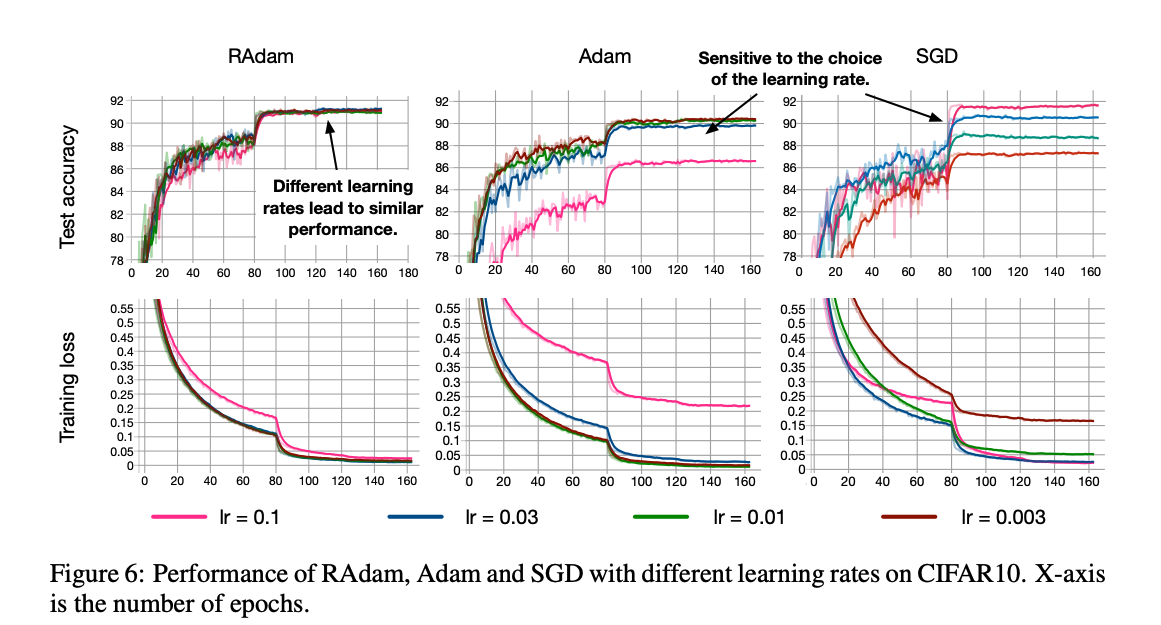
これを見ると RAdam がどのパラメータに対しても学習がうまく進んでいることが一目瞭然です.
次の実験はヒューリスティックな warm start と RAdam の戦略の差分を見るための実験です.

RAdam はいい感じに warm start をする方法, と捉えられますから RAdam が有効に働いていることが見て取れます.
他にも論文中での近似がうまくいっているかどうかの実験なども乗っています, が力尽きました.
結論と感想
Adam など adaptive な手法と同時に使われる warm start をうまく最適化のフローに取り込んだ RAdam という手法を紹介しました. 結果を見る限り warm start は必要ないような結果となっており, 職人芸的な LR 設定がひとつなくなって幸せなのかなと思いました.
また本論と関係ありませんが, この論文自体は microsoft のインターンの方が書かれたようでインターンでこれするんかというレベルの高さを感じました.
個人的な感想として以前紹介した Adabound が全く流行っていないのでこっちは流行ってほしいかなーと思いました.(warm start というヒューリスティックな方法をリプレイスできるというのは Adabound のSGDとの連続的な接続よりもインパクトがあるとも思いますので.)