FFT を使った時系列データ解析
今回は音声データやセンサーといった波形データの解析によく使われるFFTを、時系列のデータにつかって傾向の分析をやってみます、という話です。
FFTとは
FFT(高速フーリエ変換) はフーリエ変換 FT の高速版です。そのままですが。 めっちゃカジュアルに言えば、フーリエ変換(FT)は波形データからどの周期でどのぐらいの振れ幅を持っているかを抽出します。 工学の振動系とかだと、ノイズが混じった観測データから物体固有の振動を取り出したりとかに使ったり、まあ色々使われます。
この記事は FFT を使ってサンプルの波形の解析をやって、最後に日経平均の特性をちょっと見てみましょう、というのが主旨になっています。
FFT Module
python でフーリエ変換のモジュールというと有名なのは numpy.fft で基本的には
fftn: 波形空間からフーリエ変換した強度空間への射影を行う関数ifftn: フーリエ変換された強度から元の波形空間へ戻す関数fftfreq: フーリエ変換した強度関数がどの周波数に対応しているかの周波数を計算する関数
の3つを使うことが多い印象です。 scipy のほうが早いらしいので変換がボトルネックになるような巨大データを扱うときは numpy からそちらに移行することも考えてみてください。
それぞれのドキュメントは https://docs.scipy.org/doc/numpy-1.13.0/reference/routines.fft.html から見れます。
実際にやってみる
まずは下準備から
import numpy as np from numpy.fft import fftn, ifftn, fftfreq import pandas as pd import matplotlib.pyplot as plt import seaborn as sns import os output_dir = './fft_vis' os.makedirs(output_dir, exist_ok=True) def save_fig(fig, name): p = os.path.join(output_dir, name) print(f'save to {p}') fig.tight_layout() fig.savefig(p, dpi=120)
サンプルデータの準備
始めにサンプルの周期的な関数を使って、動作を確認してみます。
仮に周期が 3 の波にランダムなノイズが乗っているものを考えてみます。
周期が 3 の波を作るためには, 適当な x に対して, $1 / 3 \times 2 \pi * x$ を計算すればOKです。
今回は周期が 3 と 0.5 の波を足し合わせたものにガウスノイズをちょっと加えたものを分析対象にします。強度はそれぞれ 1, 0.7, 0.3 としています。
# データの総数 n_samples = 300 # 単位時間あたりに, いくつのデータ点が存在しているか. sampling_rate = 10 # サンプルデータ作成のために, 1 / sampling_rate ごとの等間隔な x を用意 x = np.arange(n_samples) / sampling_rate # 作成した x を入力として, 周期 3 と 0.5 の波形 (+ノイズ) を足し合わせる. y = np.sin(1 / 3 * 2 * np.pi * x) + .7 * np.sin(2 * 2 * np.pi * x) + .3 * np.random.normal(size=n_samples) # あとでの遊びのために 10 のところでわざとピークをつける y += np.where(x == 10, 5, 0)
fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, y) ax.set_title('サンプル波形')

実際にフーリエ変換してみます。
フーリエ変換する関数は fftn です。普通に使うには波形データを代入すればOKです。
出力は周波数ごとの強度になっているので、どの周波数に対応するか計算する必要があります。
これを助けてくれるのが fftfreq です。波形データの総数とサンプリングレート (Hz) を d に代入します。
d は一秒間のデータ数の逆数であることに注意して下さい。
z = fftn(y)
freq = fftfreq(n_samples, d=1 / sampling_rate)
FFT の出力のみかた
FFT は元の空間の出力値から, 各周波数ごとの強度に変換します。
一般に横軸に周波数もしくは周期をとり、縦軸にその周波数での強度を取ることが多いです。
強度各周波数ごとに出力されますが, どのぐらい綺麗な sin からずれているかの位相遅れ成分が含まれている為, 複素数で表現されています。そのため強度として表示する際には絶対値を取ることが多いです。またその際 logscale にして表示するのが一般的です。(マグニチュードとかと同じ)
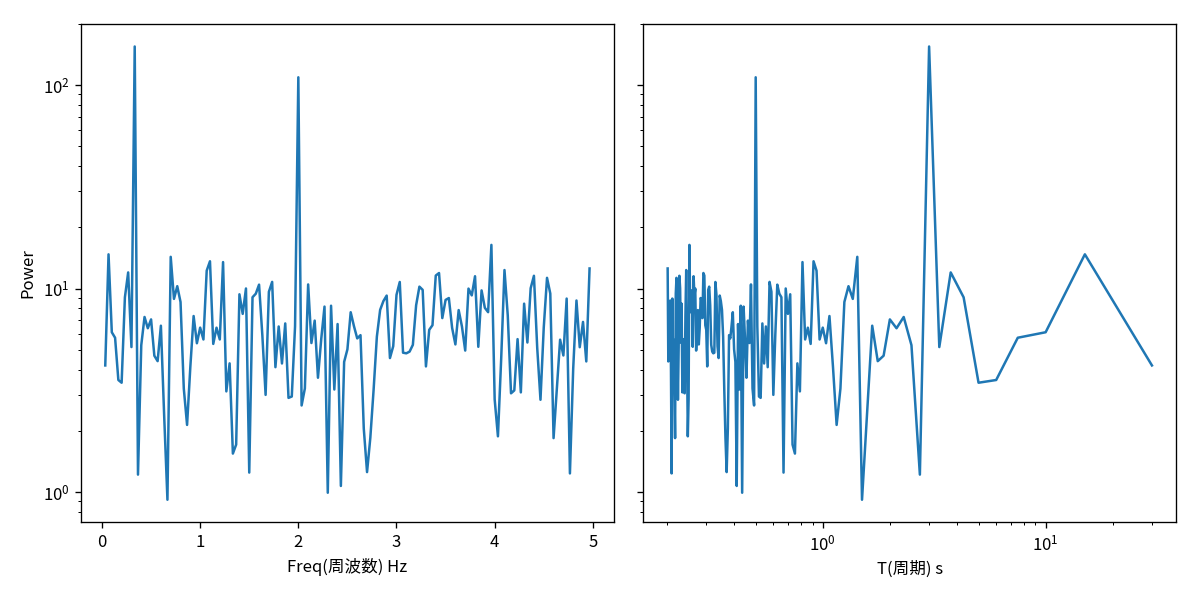
# ノリのような表示 # plt.plot(freq, abs(z)) #plt.yscale('log') # 適当にやるとマイナスの周波数も表示される. +-で値は同じ(y軸対象)なのでプラス部分だけ可視化すれば十分 # 真面目に fig, axes = plt.subplots(figsize=(10, 5), ncols=2, sharey=True) ax = axes[0] ax.plot(freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('Freq(周波数) Hz') ax.set_ylabel('Power') # 周波数 f → 周期 T に直して表示する # 周期は fT = 1 を満たすので単に逆数にすれば良い ax = axes[1] ax.plot(1 / freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('T(周期) s') ax.set_xscale('log') save_fig(fig, name='sample_wave_fft.png')
fft_pow_df = pd.DataFrame([1 / freq[1:int(n_samples / 2)], np.log10(abs(z[1:int(n_samples / 2)]))], index=['T', 'log10_power']).T fft_pow_df.sort_values('log10_power', ascending=False).head(10)
| T | log10_power | |
|---|---|---|
| 9 | 3.000000 | 2.189058 |
| 59 | 0.500000 | 2.037770 |
| 118 | 0.252101 | 1.214322 |
| 1 | 15.000000 | 1.167947 |
| 20 | 1.428571 | 1.155673 |
| 32 | 0.909091 | 1.133798 |
| 36 | 0.810811 | 1.129822 |
| 148 | 0.201342 | 1.098518 |
| 122 | 0.243902 | 1.090790 |
| 31 | 0.937500 | 1.087703 |
np.log10(1 / 0.7)
0.15490195998574316
考察
ちゃんと周期が 3 と 0.5 のところにピークが有ることがわかります。
ログスケールでの強度の差分は大体 0.15 で作成した時の強度の比の log10 の値 log_10(1/.07) とほぼ一致していることも確認出来ます。
IFFT (逆フーリエ変換)
フーリエ空間の波形強度から元の波形空間へ戻すこともできます。べんりですね。これを逆フーリエ変換(Inverse FT: IFT) といいそれを高速にするので IFFT (Inverse Fast FT) です。 フーリエ変換したあとの情報すべてを使うと、完全に元通りにすることが出来ます。
この時戻した値の実数値成分
realをつかうのをお忘れなく。ifftの返り値は数値計算の誤差で、微妙に複素数成分が含まれた値が帰ってくるので実数値だけを取り出すようにします。(ノルムにしてもいい気がするけれどまあほぼ誤差なので気にしなくても良い?)
fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(ifftn(z).real, label='IFFT') ax.plot(y, label='Original') ax.legend() save_fig(fig, name='sample_wave__ifft.png')

Low Pass Filter
先の IFFT では変換した z をすべて使って元に戻しました。ですのでまったく同じ波形になりました。
ここで, Low な frequency の周波数成分のみを使って IFFT しましょうというのが Low Pass Filter です。
要するに FFT した結果のうち, 周波数が一定以下のゆったりとした波形のみをつかって(反対に言うと高周波の凄い急な振動は消して), もとの波形空間に戻すという方法です。
これをすることで波形全体の中から細かい揺れの成分を消すことができるので、波形全体の大まかな傾向をつかむことが出来ます。
一般にセンサーのノイズとかはホワイトノイズ (np.random.norm) になるためこの影響を小さくして、センサーでとりたい対象本来の波形を抽出するのに使われたりします。
全体の傾向を取ったような関数になるので移動平均と似たなものになる。短期的な変動が消えるので簡易的な異常値検知には使えるかもしれません。
*1
ためしに先ほどわざと混入させた x=10 の場所での異常値を検出してみましょう。
# 2以下の周期を無視する様な lowpass threshold_period = 2 threshold_freq = 1 / threshold_period z_lowpass = np.where(abs(freq) > threshold_freq, 0, z) y_lowpass = ifftn(z_lowpass).real fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, y, '-', label='Original', alpha=.5) ax.plot(x, y_lowpass, label='LowPass') ax.set_title('Low Pass Filter') ax.legend() save_fig(fig, name='sample_wave__lowpass.png')

異常値が見たければ元の値と lowpass の差分を見れば良いので適当に引いて絶対値にします。
diff = abs(y_lowpass - y) fig, ax = plt.subplots(figsize=(10, 4)) ax.plot(x, diff) ax.set_ylabel('diff btw lowpass and original') save_fig(fig, name='sample_wave__diff_lowpass.png')

print(x[np.argmax(diff)])
10.0
ちゃんと 10 のとこに一番異常な点が有ることがだせました。嬉しい:D
発展: 日経平均の分析
以上で試したことを日経平均の分析に適用してみましょう。 データは [https://indexes.nikkei.co.jp] さんよりお借りした日経平均株価をつかいます。
url = 'https://indexes.nikkei.co.jp/nkave/historical/nikkei_stock_average_daily_jp.csv' nikkei_df = pd.read_csv(url, encoding='shift_jis')
# 最終行は著作権に関する情報なので、分析には使わないように。 nikkei_df = nikkei_df.iloc[:-1, :]
nikkei_df.head()
| データ日付 | 終値 | 始値 | 高値 | 安値 | |
|---|---|---|---|---|---|
| 0 | 2016/01/04 | 18450.98 | 18818.58 | 18951.12 | 18394.43 |
| 1 | 2016/01/05 | 18374.00 | 18398.76 | 18547.38 | 18327.52 |
| 2 | 2016/01/06 | 18191.32 | 18410.57 | 18469.38 | 18064.30 |
| 3 | 2016/01/07 | 17767.34 | 18139.77 | 18172.04 | 17767.34 |
| 4 | 2016/01/08 | 17697.96 | 17562.23 | 17975.31 | 17509.64 |
一旦可視化してみましょう
nikkei_df['データ日付'] = pd.to_datetime(nikkei_df['データ日付']) nikkei_df = nikkei_df.set_index('データ日付') fig, ax = plt.subplots(figsize=(len(nikkei_df) * .02, 5)) nikkei_df.plot(ax=ax)
これを見ると若干 FFT の仮定である定常的な波 (一定周期で同じ波形を繰り返す) が成り立っているか微妙ですね… 特に始めと終わりの値が結構ずれているので端点で相当無理が生じそうです。
FFTでは波形に周期があることが仮定されています。ですので今回の日経平均の用に入力データの端点が揃っていない場合、その仮定が成り立たず正直かなり良くありません。
この補正をするのが窓関数で hamming 窓などが有名です。(窓関数を使う理由に関しては https://www.logical-arts.jp/archives/124 がとても詳しいです。)
今回はローパスフィルタを作りたいというのもあるので一旦窓の適用はせずに分析しますが以下の分析結果は眉唾で聞いて下さい
系列はほとんどすべて同じなので終値を使うことにします。
y = nikkei_df['終値'].values # 窓関数使うときは window を作って掛け算. # y = y - np.mean(y) # window = np.hamming(len(y)) # y = y * window x = nikkei_df.index
n = len(y) z = fftn(y) # 単位時間は日でサンプリングレートも1なので `d=1` を指定 freq = fftfreq(n, d=1)
fig, axes = plt.subplots(figsize=(10, 5), ncols=2, sharey=True) ax = axes[0] ax.plot(freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('Freq(周波数) Hz') ax.set_ylabel('Power') ax = axes[1] ax.plot(1 / freq[1:int(n_samples / 2)], abs(z[1:int(n_samples / 2)])) ax.set_yscale('log') ax.set_xlabel('T(周期) s') ax.set_xscale('log') save_fig(fig, name='nikkei_fft.png')

nikkei_pow_df = pd.DataFrame([1 / freq[1:int(n_samples / 2)], np.log10(abs(z[1:int(n_samples / 2)]))], index=['T', 'log10_power']).T nikkei_pow_df.sort_values('log10_power', ascending=False).head(10)
| T | log10_power | |
|---|---|---|
| 0 | 860.000000 | 6.098400 |
| 1 | 430.000000 | 5.461296 |
| 2 | 286.666667 | 5.456172 |
| 4 | 172.000000 | 5.416735 |
| 5 | 143.333333 | 5.220405 |
| 6 | 122.857143 | 5.212416 |
| 7 | 107.500000 | 5.128081 |
| 3 | 215.000000 | 5.068687 |
| 9 | 86.000000 | 5.033504 |
| 17 | 47.777778 | 4.920812 |
周波数成分からわかること
- 長周期の成分が大きそうです。定期的な繰り返しというよりは大きく平均値が変わるような変動をしているといえます。
正直その程度はぱっと見れば誰でもわかりますがそれを定量的に評価できているのは良い点かもしれません。 - 意外と一週間とか一ヶ月の周期は出てこない。月曜日だから買う!とかいう人は居ないんですね(当たり前)
ついでに Low Pass Filter もやってみましょう
# 30日以下の周期を無視する様な lowpass threshold_period = 30 threshold_freq = 1 / threshold_period z_lowpass = np.where(abs(freq) > threshold_freq, 0, z) y_lowpass = ifftn(z_lowpass).real fig, axes = plt.subplots(figsize=(10, 8), nrows=2, sharex=True) ax = axes[0] ax.plot(x, y, '-', label='Original', alpha=.5) ax.plot(x, y_lowpass, label='LowPass') ax.set_title('Low Pass Filter') ax.legend() ax.set_ylabel('日経平均終値') diff = y_lowpass - y ax = axes[1] ax.plot(x, abs(diff)) ax.set_ylabel('LowPassFilterとの差分') ax.set_xlabel('日付') fig.tight_layout() save_fig(fig, name='nikkei_diff_lowpass_and_original.png')

やはり周期性が成り立っていないものに対して端の値を合わせようとしているために 2016-01 と 2017-07 の値は差分が大きいです。やっぱり日経平均に適用するのはむりがあったかも…反省…
このような端点も見るためには、局所的な情報を使うスペクトログラムとか使う必要がありそうです。(スペクトログラムは局所的な幅 (window) の中で FFT をいくつもやるようなイメージです。なので波形全体で周期性がなくてもその場その場での傾向を可視化出来ます。やってからこれはFFTのお仕事ではないなと)
端を除外して, ぱっと目立つのは 2016年にひとつ有る大きな暴落と2019年になるあたりでの急上昇と急降下でしょうか。
_df = pd.DataFrame([diff, x], index=['diff', 'date']).T.sort_values('diff', ascending=False)
_df.head(10)
| diff | date | |
|---|---|---|
| 27 | 1345.16 | 2016-02-12 00:00:00 |
| 209 | 1199.49 | 2016-11-09 00:00:00 |
| 733 | 1155.33 | 2018-12-25 00:00:00 |
| 12 | 1044.84 | 2016-01-21 00:00:00 |
| 5 | 998.391 | 2016-01-12 00:00:00 |
| 0 | 981.503 | 2016-01-04 00:00:00 |
| 3 | 910.682 | 2016-01-07 00:00:00 |
| 734 | 907.997 | 2018-12-26 00:00:00 |
| 514 | 859.389 | 2018-02-06 00:00:00 |
| 1 | 802.091 | 2016-01-05 00:00:00 |
_df.tail(10)
| diff | date | |
|---|---|---|
| 854 | -866.97 | 2019-07-01 00:00:00 |
| 18 | -922.626 | 2016-01-29 00:00:00 |
| 76 | -1031.42 | 2016-04-22 00:00:00 |
| 855 | -1099.33 | 2019-07-02 00:00:00 |
| 856 | -1208 | 2019-07-03 00:00:00 |
| 20 | -1247.26 | 2016-02-02 00:00:00 |
| 19 | -1318.26 | 2016-02-01 00:00:00 |
| 857 | -1510.47 | 2019-07-04 00:00:00 |
| 858 | -1802.45 | 2019-07-05 00:00:00 |
| 859 | -1844.78 | 2019-07-08 00:00:00 |
まとめ
波形データの特性を見るのに使われる FFT の使い方をざっくり紹介しました。 使ったデータに定常性が対してなかったこともあり、今回はあまり良い傾向の分析は出来ず残念でしたが、系列データの特性を数値的に表現できる便利ツールなので、EDAとかに使うと説得力があってよいかなーと思います。
*1:もちろんこれは相当不真面目な異常検知です。真面目にやるときは系列データの生成モデルなりを仮定して、生成される確率が小さい時にアラート、などやる必要があります。
Adabound の final_lr と収束性について
みなさん optimizer は何を使っていますか? (僕は SGD + Momentum + Nesterov が好きです)
adagrad/adadelta/adam などなど NN で用いられる optimizer は数多くありますが, 最近提案された optimizer に adabound というものがあります。 adabound はざっくりいうと SGD と adam のいいとこ取りを狙った手法で、論文では序盤では adam の早い収束性を, 終盤では SGD の高い汎化性を再現しています。

自分のスライドで恐縮ですが Adabound やそのたの Optimizer について解説したものがあるのでもしよければ参考にしてください。
確率的勾配法のはなし https://t.co/UUTvQSII3F 今日のもくもく会のスライドです。確率的勾配法のお話をしました。
— ニューヨーカーGOTO (@nyker_goto) 2019年4月17日
final_lr ?
つよつよな Adabound ですが新しく final_lr というパラメータが追加されています。 これは学習終盤での lr の上界と下界を決定するパラメータです。適当に手元のタスクで数回実験をしてみたところ lr + final_lr が結果に大きく影響しているように感じられました。
そこで今回は超解像度化モデル ESPCN の学習を使って lr と final lr がどのような関係になっているのかを実験してみました。
実験条件
実験は前回の画像の超解像度化モデル ESPCN(画像の超解像度化: ESPCN の pytorch 実装 / 学習 - nykergoto’s blog) を使います。前回は adam で学習をしていましたが、それを adabound で置き換えます。
lr の探索範囲
上記の実験では Adam の最適な学習率は 0.001 でした。よってその周辺が良いでしょうという仮定をおいて LR の探索は $10^{-2.5} \sim 10^{-4}$ まで底を10に取ったログスケール上で 0.5 刻みで動かします。
final_lr の探索範囲
final_lr に関しては、元の論文でも言われているように adabound は最後の段階で SGD に近い動きをすることが狙いでした。SGD の最適な学習率はおおよそ 0.01 程度の値でしたので、それを考えるとだいたい 0.1 ~ 0.001 ぐらいで動かせば良さそうに思えます。
しかし adabound で用いている勾配は SGD のそれではなく Adam のものと同じです。Adam では過去の勾配を指数加重平均を取ったものを更新につかいます。
この勾配は過去情報を使って平均化していますから、 SGD で用いている「単なるステップ $t$ で得られた勾配 $g_t$」に比べて分散の少ない勾配、言い方を変えると FG*1 をより上手く近似できている「良い」勾配となると期待できます。
特に final lr が active になるような学習の終盤ではよりその傾向が顕著になるはずですので final lr もそれに合わせて大きめにとっておくのが良いのではないか? とも思えます。
この仮説をもとにして final lr の探索範囲は SGD の最適 lr に比べて大きめな範囲も含めるように 10 ** 0.5 ~ -2 まで 0.5 刻みで学習をさせました。
その他の条件
通常のNNの学習同様 lr を一定 step ごと(今回は 15epochごと) に 0.1 倍する schedule で学習します。 training データと validation データは別のデータセットを使いこれらは先の記事と同様の物を使います。 評価指標は目的関数にも用いている mse で評価しました。
結果
各条件ごとでの training mse の最小値を lr を縦軸に, final_lr を横軸にとってヒートマップとして表したのが以下の図です。

各セルが横軸の LR と縦軸の final_lr の時の rmse の値を表しています。色が明るいほど小さい、すなわち mse の小さい良い解です。 (縦軸横軸ともにログスケールになっていることに注意して下さい)
これを見ると final_lr の影響のほうが支配的であり final_lr が大きい値のほうが mse の値を最小化できていることが確認できます。
adabound の pytorch 実装 https://github.com/Luolc/AdaBound の初期値では final_lr=0.1 になっています ので、それよりも大きい値を設定してあげる必要がありそうです。
同様のことを validation データについてプロットしたのが以下の図です。こちらも training mse 同様の傾向があることがわかります。

まとめと感想
ESPCN モデルを使った実験を行ったところ final_lr の値が loss の最小値を決めており lr は余り影響していないことがわかりました。 adabound の論文では「 lrに左右されずに収束が早まる」という意味の主張がされていましたのでそれが裏付けられた形になりました。
一方で final_lr を SGD の最適値よりもかなり大きい値に設定していないと, 良い解に収束しない様子が確認されました。 このことから adabound を使う際には SGD よりも大きめの final_lr, 具体的には 0.1 やもうちょっと大きい値 (今回でいうと 1.0 ぐらいのほうが性能は良かった) を使って置く必要がありそうです。
[Future Work] 🤔
上記色々書きました、がこれは単に ESPCN モデルを mse で最適化した時にそうなった、ということに過ぎません。 超解像度化のモデルは、体感でも相当収束が早い簡単なモデルです。そのため指数平均を取った勾配の Variance が相当抑えられ大きな LR を取って更新する必要があった可能性も否めません。 要するにこの結果が一般に言えるかどうかは微妙なところなので、もうちょっと調べてみたいところです。😌
今後やりたいこと
- 物体認識とかで adabound を使って同じような傾向があるかどうかを調べる
参考文献
*1:目的関数全体の勾配 Full Gradient のことです。データすべての勾配の平均、といってもOKです。
画像の超解像度化: ESPCN の pytorch 実装 / 学習
画像の超解像度化シリーズ第二弾です。 第一弾 では NN を使ったモデルの中では、もっとも初期 2015年に提案された SRCNN を実装しました。今回はそれから一年後 2016年に提案された ESPCN を実装して学習させてみたよ、という話です。
ESPCN は Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network という論文で提案された手法です。こちらも SRCNN 同様画像の特徴抽出機構として CNN を使っていますが若干の変更点があります。順に紹介していきます。
ESPCN 概要
SRCNN のモデルは入力と出力の画像サイズが同じようなモデルでした。そのため特定の画像を $r$ 倍の画像へ超解像度化したい場合には
- 元の画像を古典的手法で $r$ 倍して拡大
- 拡大された画像をネットワークへ入力
という流れをとっていました。一方で ESPCN ではロス関数は同じく MSE ですが入力画像は直接拡大されるという点が異なります。実際にネットワークを表したのが以下の図になります。

入力された $W \times H$ サイズの画像は3層のCNNにより $r^2$ のチャネルを持つ3次元テンソルへと変換されます(この時画像の高さと幅の大きさは変化させないように padding なりを用意します。) その後 PixelShuffle と呼ばれる機構によって $rW \times rH$ の大きさへと変換されます。
pytorch のネットワークで表現すると以下のようになります。
class ESPCN(AbstractNet): only_luminance = True input_upscale = False def __init__(self, upscale=2): super(ESPCN, self).__init__() self.upscale = upscale self.conv1 = nn.Conv2d(1, 64, kernel_size=5, stride=1, padding=2) self.conv2 = nn.Conv2d(64, 64, kernel_size=3, stride=1, padding=1) self.conv3 = nn.Conv2d(64, 32, kernel_size=3, stride=1, padding=1) self.conv4 = nn.Conv2d(32, upscale ** 2, kernel_size=3, stride=1, padding=1) self.pixel_shuffle = nn.PixelShuffle(self.upscale) def _initialize_weights(self): weights_with_relu = [ self.conv1.weight, self.conv2.weight, self.conv3.weight ] for w in weights_with_relu: nn.init.orthogonal_(w, nn.init.calculate_gain('relu')) nn.init.orthogonal_(self.conv4.weight) def forward(self, x): h = F.tanh(self.conv1(x)) h = F.tanh(self.conv2(h)) h = F.tanh(self.conv3(h)) return self.pixel_shuffle(self.conv4(h))
ESPCN の肝: PixelShuffle
この最終層で用いられている PixelShuffle はこの論文で提案された新しい画像の拡大方法です。それまでは画像の拡大には DeConvolution を用いられることが多かったのですが、この演算は単に CNN を逆方向に行うだけなので画像に周期的ができるような現象が観測されることがありました。 Deconvolution の問題点は Deconvolution and Checkerboard Artifacts などが詳しいです。
PixelShuffle では拡大したい倍率を $r \in \mathbb{N}$ とした時 $r \times r$ のチャネルを直前の層で用意して、それらを1チャネルの上にタイル状に並べることで画像の拡大を行います。
例えば拡大率を 3 として元画像サイズが 1x1 だとします。このとき出力層の前の層では 9 チャネルを持つ 1x1 のテンソルを用意しておきます。これを $x \in \mathbb{R}^{1 \times 1 \times 9} $ と置きましょう。この時 PixelShuffle の出力 $y \in \mathbb{R}^{3 \times 3}$ は
$$ y_{i,j} = x_{1, 1, i + (j - 1) \times 3} $$
になります。特徴は出力がすべて元のテンソル成分によって決まっておりかつ元のテンソル要素が出力に寄与する部分がひとつしかない (i.e. overlap がない)という点です。これによって出力がゆがんでしまうことを防ぐことが出来ます。
その他変更点
その他の重要な変更点としてはネットワークに通す画像は RGB の 3チャネルの画像ではなく輝度情報のみの1チャネルの画像のみを用いるという点があります。これは人間が画像のクオリティを判定する際には輝度情報を重要視する、という部分から来ているようです。 他の2色の情報は古典的な手法で拡大し、最終的にマージして RGB に変換する、という処理を行います。
この処理は PIL.Image インスタンスに対してならば以下のように行なえます。
def get_luminance(img): x, _, _ = img.convert('YCbCr').split() return x
また PixelShuffle の構造上ネットワークの出力は元の画像の $r$ 倍でないといけない、という制約がある点も実装を行う上では注意する必要がある点です。要するに復元する画像は縮小された画像の $r$ 倍である必要があるため割り算できない大きさの画像は扱えないのです。そのため画像の大きさから拡大率で割り算できる最大の整数を返すような関数を定義しました。
def calculate_original_img_size(origin_size: int, upscale_factor: int) -> int: """ 元の画像サイズを縮小拡大したいときに元の画像をどの大きさに resize する必要があるかを返す関数 例えば 202 px の画像を 1/3 に縮小することは出来ない(i.e. 3の倍数ではない)ので 事前に 201 px に縮小しておく必要がありこの関数はその計算を行う すなわち calculate_original_img_size(202, 3) -> 201 となる Args: origin_size: upscale_factor: Returns: """ return origin_size - (origin_size % upscale_factor)
実験
今回も数値実験を行ってみます。実装のコードは以下からアクセス出来ます。
実験条件は以下のとおりです
環境
- Intel(R) Core(TM) i7-7700K CPU @ 4.20GHz
- GEFORCE GTX 1080
- Ubuntu 16:04
学習/検証 データセット
BSDS3000 データセットを用いました. 含まれる画像が300枚と少ないので random clip / horizontal flipping を行い水増ししています。1epochの定義は 100000 images と定義しています。 拡大のスケーリングは3倍としました。ですので、学習時にはもとの画像を 1/3 に縮小した画像を入力とし、出力を元の画像と合わせるように学習を行います。
検証用データセットには前回同様に Set5 を用いました。
最適化
最適化手法は Adam/SGD/Adabound 各々でパラメータの組み合わせでグリッドサーチを行いました。
ここですべての Optimizer に共通な条件として epoch=45 / 15 epoch ごとに 0.1 倍の lr decay, weight_decay=1e-8 と設定しています。
以下で結果に示すモデルは Validation Loss が最も良かった Adam (lr=1e-4, weight_decay=1e-8) を用いて学習されたものです。
一回の学習はだいたい 30 分程度です。 データの加工部分に画像を都度 random clip して縮小するというまあまあ重たい処理が入っているので, workers=4 程度だとGPU 律速ではなく CPU 律速になっているように見受けられました。逐次水増しせず事前に切り出しておくなどしておくべきだったかもしれません。
結果
実際に学習されたネットワークを用いて超解像度化を行ってみます。Set5 のなかではもっとも復元が難しい(bicubicでのRMSEが最も低い) butterfly を用います。実際に超解像度化を行ったのが以下の図です。

BICUBIC に比べると ESPCN では黒い部分の境界が鮮明に復元できていることがわかります。
おまけ
学習/Validation データのロス/PSNR の遷移は以下の様な感じ。ほぼ同じような動きをしているので学習はできていることがわかります。

まとめと感想
SRCNN の次世代アーキテクチャ ESPCN を紹介しました。この手法の肝は PixelShuffle で、入力画像が直接拡大される、輝度情報以外はネットワークでは扱わないのが変わった点です。
本当は SRCNN の結果と比べたい、のですがこれを書いている時に SRCNN の実験を x2 で行っていたことに気がついてしまい乗せられませんでした。今から実験します…
個人的に面白いなと思ったのは ESPCN では adam が一番よかった、という点です。 SRCNN では一番良かったのは SGD + Nesterov + Momentum で, adam は training loss は一番下がるが汎化せず(Validation Data のロスが全く下がらない)過学習に陥っていました。おそらく原因はネットワークの構造が単純すぎるため、すぐに最適解にたどり着けてしまう adam では局所解にハマってぬけだせなくなるからかなーと推察していました。
よりネットワークが複雑な ESPCN では adam が一番汎化することからも、上記の仮説はあっているような気がしています。単純すぎるときはゆっくり最適化するほうがいいのは面白いですね。
次やりたいこと
2016年まで来た。もうちょっと未来にいく。次はGANをつかった人間が見た時に自然な復元を試みている手法を実装したい。
参考文献
- Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel Convolutional Neural Network
- leftthomas/ESPCN
pytorch espcnでググった時に一番上に出てくる実装。最終的な出力に sigmoid を掛ける処理が入っているのですが論文中にその記述が見つからなかったので僕の実装ではそのままを出力にしています。
画像の超解像度化をするモデル SRCNN を pytorch で実装してみた
画像の超解像度化というタスクがあります。 やることは低解像度(小さい画像)を高解像な画像に拡大するときにできるだけ綺麗に引き延ばす、というタスクです。
https://www.slideshare.net/HHiroto/deep-learning-106529202 ではDeep Learning の登場によって超解像度化技術がどのように進歩していったのかに関してとてもわかり易くまとまっていて良いです。
その中でも Deep Learning の活用が始まりだした 2015 に登場した SRCNN というモデルを実装してみました。
SRCNN の構造
SRCNN のアーキテクチャは3層の Convolution + Relu で構成されています。pytorch だと以下のような感じでとてもシンプルです。
from torch import nn class Generator(nn.Module): def __init__(self): super(Generator, self).__init__() self.conv1 = nn.Conv2d(in_channels=3, out_channels=64, kernel_size=9, padding=4) self.conv2 = nn.Conv2d(in_channels=64, out_channels=32, kernel_size=1, padding=0) self.conv3 = nn.Conv2d(in_channels=32, out_channels=3, kernel_size=5, padding=2) self.activate = nn.ReLU() def forward(self, x): h = self.activate(self.conv1(x)) h = self.activate(self.conv2(h)) return self.conv3(h)
ちょっと注意なのは、このネットワークでは入力される画像サイズと出力される画像サイズは同じだということです(このネットワークでは拡大はしません)。 入力されるのは低解像度画像を拡大した荒い画像で、それを同サイズの綺麗な画像にして返すというふうになっています。
学習時には、綺麗な画像と荒い画像のペアのデータが必要になります。
元の論文では、元の画像に対してガウシアンぼかしを適用して荒い画像を生成していました。
なんですが色々と実装を見ていると、画像を半分など小さく縮小して古典手法で拡大する、という方法をとっているものが大半だったので実装ではこちらを採用しています。
どれだけ綺麗に戻せたかのロス関数にはピクセル間の MSE を用います。
実装
Github にあげています。詳しくは readme に書いていますが docker/docker-compose が入っていれば動かせる、はず
実験
実際に上記の実装を使って学習を回して、超解像度をやってみました。
データセット
学習につかうデータセットはSRCNN 論文に合わせて Anchored Neighborhood Regression for Fast Example-Based Super-Resolution で使われている 91 枚の画像をつかいました。実際にはこれらの画像を 64x64 の大きさにランダムに切り出しています。
検証には Set5 と呼ばれている画像をつかいました。いろんな論文に登場するので、この分野ではよく使われるデータセットみたいですね。
実験
学習したモデルを使って実際に超解像度化を行います。左が元画像を半分に縮小して人工的に作った低解像度画像、真ん中が SRCNN で綺麗にした画像、右が元の画像です。低解像度画像は x0.5 にリサイズした後 BICUBIC で拡大して作成しました。


これだとちょっとわかりにくいので画像の一部分を拡大してみます。

感想
モデルがとても単純なわりに、しっかり綺麗になるのでやはり CNN の構造はとても良い性質を持っているんだなと改めて思いました。
モデルが小さいので推論だけならば CPU で十分動くので、既存のサーバーとかにも組み込みやすいように思えます。計算量が軽いことを活かして、フロントエンド側で画像を勝手に綺麗にして表示するとかも面白そうです。
あと実装的な観点でいうと torchvision の transform がとても便利で、画像の拡大縮小のコードがとってもすっきりかけて気分が良かったです😄
気になった点としてはネットワークに BatchNormalization がないので若干学習が不安定になりがちな点ですが、これは BatchNormalization が出来たのが 2015 年なので当たり前でした。Deep 界隈の進歩の速さを象徴しているなーとあらためて思いました。
つぎやりたいこと
- 今僕は 2015 年にはこれたので, もうちょっと未来のアーキテクチャを実装して差分をみてみたい
参考文献
- Image Super-Resolution Using Deep Convolutional Networks Chao Dong, Chen Change Loy, Kaiming He, Xiaoou Tang
- SRCNN を提案した論文です。
- Anchored Neighborhood Regression for Fast Example-Based Super-Resolution
- Anchored Neighborhood Regression という拡大手法を提案した論文です。学習にはこの論文で使われた学習用画像を用いています。
