2018-11-28

敵対的サンプリング検出のための基準としての相互情報量 - Understanding Measures of Uncertainty for Adversarial Example Detection

論文機械学習

Understanding Measures of Uncertainty for Adversarial Example Detection
https://arxiv.org/pdf/1803.08533.pdf

概要 (200文字程度)

敵対的サンプルを判別する基準として相互情報量 (Mutual Information) が優れていることを主張する論文. MI の推定に Dropout を用いた MC を採用している.

Mnist と隠れ層2次元 Variational Autoencoder を用いて不確実性の分布を可視化し既存の基準である softmax entropy と MI の違いをわかりやすく説明している.

この論文の新規性

予測の不確実性を意味によって2つに分離し、モデルの知識不足部分の不確実性を取り出せれば敵対的サンプルを判別できるという主張を情報量の観点から議論している点.

不確実性の基準

そもそも不確実な入力には2つの種類がある

知識不足による認知の不確実性
データの偶然性による不確実性

機械学習の文脈で言うと、前者はデータが欠乏しているために、その入力データに対する事後分布が平らになってしまうような現象を指す。

後者はそもそも入力データに対して出力のばらつきが激しくて予測が無理な場合を指す。例えば表も裏も確率 1/2 で出るコイン投げの予測モデルなどは、知識ではなくデータの生成過程自体が完全にランダム性に支配されている為に起る不確実である。

一般に用いられる不確実性を測る基準として、予測値と入力のエントロピーがある。

$$ H[p(y | x)] = - \sum_{y \in Y} p(y| x) \ln p(y | x) $$

ここで $Y$ はモデルの予測値が取る離散的な空間を表している。この基準は先の2つの不確実性を分離していない為、不確実性がモデルの知識不足から来るのか、それともデータの分散が激しいことから来るのかに関して判断することはできない。

そこでデータ $D$ と入力 $x$ が与えられた時のモデルのパラメータ $w$ とその予測値 $y$ の相互情報量 (Mutual Information) を考える。これは以下の式で表される。

$$ I(w; y | x, D) = H[p(y|x, D)] - {\mathbb E}_{p(w|D)}[H[p(y|w,x)]] $$

A, B の相互情報量とは B の情報を得た時に減少するAの不確かさのこと、と解釈することができる(A, B は逆でも成り立つ)。

今回でいうと、ラベル $y$ が与えられた時に減る $w$ に関する不確かさである。これは即ち $w$ に関して新しく得られた情報量とみなすことができる。

相互情報量が大きいような $x$ はどういう値かということを考えてみる。相互情報量が大きいとは上記の議論より、得られる情報量が大きいということであるから、そのラベルの値 $y$ の価値が大きい(ひとつの $y$ を得るだけでとても大きな情報(知識)を得ることができる)。一方で相互情報量が小さいというのはラベルの価値が小さい、すなわち既にその入力 $x$ に対する $w$ の不確かさが十分に小さく、ラベルを与えられてもあまり情報が増えないということを表している。

よってこの相互情報量は、先の「不確実性の種類」で言うところの知識不足による不確実性(1) に相当する量である、とみなすことができる。

この情報量は直接的に計算できないが Dropout を用いた MC をすることで近似的に求めることが可能である。具体的にはラベルの事後分布を

$$ p(y|D,x) \simeq \frac{1}{T} \sum_{i=1}^T p(y|w_i, x) := p_{MC} (y|x) $$

の用に近似することで以下のように計算することができる

$$ I(w; y | x, D) \simeq H[p_{MC}(y | D, x)] - \frac{1}{T}\sum_{i=1}^T H[ p(y|w_i, x)] $$

不確実性の基準による違い

相互情報量であれ予測値のエントロピーであれ、入力画像 $x$ の分布(多様体)から著しく離れた $\hat{x}$ が与えられると大きな値を取る。一方で予測値のエントロピーは入力画像 $x$ の分布(多様体) の近くであっても大きな値を取る場合がある。これはそういう画像が本質的に曖昧なもの, すなわちラベルがつけにくいものであるからである。

例えば人間が見ても 1 とも 7 とも見えるような画像があるとする。これは本質的に 1 or 7 が決定的に決められない曖昧な画像であるから予測値の softmax の値は複数のラベル（今回であれば 1 と 7) の確率が高い予測となる。エントロピーはひとつのラベルにピークを持つものほど小さくなる性質を持つので¹、このような一つに決められないものに対してはエントロピーは大きくなる。一方でMIは低い値を保つ(MIは (2) を測るものであるからである)。

さらに、敵対的サンプルとは元画像の持っているクラスとは別のクラスを持つ画像を作る行為であり、普通元のクラスの予測値を小さくし、高くしたいクラスの確率を大きくするように画像を修正する。

これは予測値のエントロピーを小さくするという効果もあるが MI によって測ることができる不確実性にも影響を与える、というのもエントロピーの下界が MI に相当するので、エントロピー最小化を行ってもMIより小さい値になることは無いからである。

MI と softmax の分散

softmax の分散と MI のテイラー展開した第一項は一致するので softmax の分散は MI の近似とみなすことができる。(詳細は論文参照のこと)

実験の対象と結果

MNIST に対して latend dim = 2 の VAE を用いて潜在空間の不確実性を可視化する実験と、犬と猫の分類問題に対する敵対的サンプルを entropy と MI とで予測しその不確実性の違いの特徴を調べる実験を行っている

MI と entropy の曖昧さの捉え方の違い

潜在空間で内挿したあと decoder を通して画像にしたものと、入力画像自体を内挿した画像とを用意してそれぞれ entropy と MI の値がどうなるかを表したのが以下の Figure2. である。

f:id:dette:20181128025644p:plain

上段の上の画像が潜在空間の内挿の画像で下が実空間上での内挿の画像を表している。
中段がそれらの entroy の値であり、下段が MI の値である。これを見ると entropy では潜在空間 (Latent Sapce) の内挿画像 (図の赤線）にたいしてピークを持っているのに対して MI ではピークがないことがわかる。これは潜在空間で内挿された画像は「不確実であるが本質的に曖昧で予測が曖昧なのは当然」な画像であるためデータの持つ偶然性も図ってしまう entropy は大きくなるが、モデルの知識に関する不確実性のみを測る MI ではそういう画像は曖昧で当然であるという判断になり小さいままなためである。

一方入力画像自体を内挿した場合 (Image Space) は entroy, MI ともにピークを持つ。これはそういう画像は訓練データに存在しておらず「この画像に対する知識は無い（言い換えるとモデルパラメータの分布の裾が広い）」ため、ラベルが与えられた時に得られる情報が大きいからである。

MNIST with VAE

隠れ層が2次元の VAE を用いて潜在空間上の点とその点での不確実性を可視化して、基準による違いを見る。やり方は

潜在空間上で適当に点を取る
decoder に通して画像空間上に射影して対応する画像を作成
作成した画像の不確実性を計算
以上を空間すべての点で計算して画像化する

という流れになっている。 fig1 が MI, fig4 が entropy の値を可視化したもの。どちらも白いところが不確実性が高い場所で黒くなるに連れて低い値となるようにプロットしている。色の付いている部分は MNIST の各クラスの画像の潜在空間上での値を表す。

f:id:dette:20181128030028p:plain f:id:dette:20181128030025p:plain

共通する傾向として中心から遠い（画像の多様体から遠い）場所では白い（＝不確実性が高い）。

一方でよーく見てみると fig4 の方は色のついたクラスの間のところが白くなっているのがわかる。これは2つのクラスの間の画像で fig2 の上段の上の画像に相当するもので「数字っぽいけど本質的に曖昧でなんとも言えない画像」に対応している。エントロピーだと不確実性を区別しないので、クラスの間は不確実性が高くなるというわけである。

もうひとつ気になるのは Dropout で不確実性をどの程度禁じできているのか、という点である。これに関しては Dropout による変分推論は局所的なモードしか捉えられない為に事後分布全体の近似としては上手く働いていない。² このため decoder によって生成された画像が意味をなしていないような場合でも高い信頼度を出してしまうような領域（holes と作者は呼んでいる)が出てしまう (figure5 がその例。 figure4 でも2時の方向に黒い holes が確認できる。)。³

このような穴があるがゆえ、敵対的サンプルはこの脆弱性をついて攻撃することが可能である。

そこで事後分布をちゃんと表現できればこの弱点を緩和できるのでは?という観点に基づいて修正を行う。具体的には Dropout モデルをいくつも作ってアンサンブルする。こうすることで事後分布の mode の一つしか表現できないという弱点を解消できる。⁴

それをやったのが以下の figure6 で figure4 と比べるとだいぶ穴が減っているのがわかる

f:id:dette:20181128030125p:plain

犬猫分類

ASSIR cat and dogs データセットを用いて敵対的サンプルがどうかの判別を行い基準ごとの性質を確認する

使用するモデル

Imagenet で訓練済みの ResNet の Convolution 層を固定し Full Connection レイヤのみを fine-tuning したモデルをつかう。 Dropout は FC 層のみに適用し、 MC は 20 サンプルを抽出する。

確定的な予測は Dropout を使わないだけで重みの値は全く同じネットワークを使用する。

敵対的サンプルのアルゴリズム

Basic Iterative Method
Fast Gradient Method
Momentum Iterative Method

の3つを使う。

結果と考察

各種の敵対的サンプリング作成法によって作られた画像の分類精度を AUC で測ったのが以下の表である。

f:id:dette:20181128030140p:plain

DETERMINISTIC と MC の違いは予測時にも dropout を使って重みの事後分布の期待値として予測をしているかどうか、である（MCがテスト時にもdropoutを行う)。相互情報量は dropout による近似を行わないと計算不能なため、DETERMINISTIC では N.A と記述されている。

結果を見ると MI が良い性能を出しておりまたエントロピーでは 0.50 を下回っている。 0.5 を下回る AUC は ランダムに判定するよりも性能が悪い ことになる。これは敵対的サンプルに対して過度に信頼度をおいていることを示している。

一方犬猫判定の精度においては、MCを用いたモデルの精度よりも確定的な値を用いたモデルの精度のほうが良いという結果になった。これは Dropout の確率が高すぎたために畳み込み層の特徴の一部しか使えずに転移学習の足を引っ張る形になってしまうのが原因と考えられるので、 dropout は精度に関しては良い影響は与えられない。

議論と結論

敵対的サンプルに対して制約を与えずにただ不確実性だけを見れば自動的に良いロバスト性を得られることを示したのは進展である。
Dropout だけが敵対的サンプルに対抗する手段であるとは思っていない。ただ確定的なモデルよりも攻撃するのが難しくなっただけ。
隠れ層の可視化でわかったことは敵対的サンプルに対抗するためには第一にモデルのロバスト性を高めて不確実性を扱えるようにすれば、結果として騙されにくいモデルが出来上がる、ということ。

読んでみた感想

VAE を用いて潜在空間を可視化し、既存の基準と提案基準の違いをわかりやすく表現していて読みやすかった。数式が出てくる論文は気分が良い。

次に読むべき論文は

敵対的サンプル系の論文読んだことないので読みたいね、ということで実験で使っていた手法一覧です。

ADVERSARIAL EXAMPLES IN THE PHYSICAL WORLD
- basic iterative method による敵対的サンプルの生成論文
EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES
- fase gradient method による敵対的サンプルの生成論文
Boosting Adversarial Attacks with Momentum
- momentum iterative method による敵対的サンプルの生成論文

最もエントロピーが小さいのはディラックのデルタ関数となる場合であり、最もエントロピーが大きくなるのはすべてのクラスの確率が同じとなる場合である。↩
これは KL距離が非対称であるがゆえ、VI が事後分布のピークの一つを近似するようなものになるという性質が原因↩
(本当は訓練データに似たものの無い画像に対しては不確実だよーと言ってほしい)↩
当然計算量はモデル数が $n$ ならば $n$ 倍になってしまうという欠点は持っている↩

2018-11-19

seaborn の clustermap をちゃんと理解する

python の可視化ツールは matplotlib が有名ですがそのプラグイン的役割を果たすモジュールとして seaborn があります。seaborn でプロットすると勝手に回帰直線をプロットしてくれたりするのですが今回は seaborn.clustermap を取り上げます。

seaborn.clustermap とは

seaborn.clustermap は入力された二次元データフレームを行と列それぞれでクラスタリングし、近いクラスタ同士を近い場所に配置するよう並び替えを行った後 heatmap + デンドログラム(樹形図)として可視化することができる関数です。

API: https://seaborn.pydata.org/generated/seaborn.clustermap.html

適当にあやめデータセットでやると以下のようになります。それっぽい図が出てきて楽しい気分になります。

import seaborn as sns
df_iris = sns.load_dataset('iris')
species = df_iris.pop("species")

g = sns.clustermap(df_iris)
g.savefig('clustermap.png', dpi=150)

f:id:dette:20181119022900p:plain

一方でこのクラスタリングがどういうロジックに基づいて動いているのか、カスタマイズするときはどうやったらええのか、ベストプラクティス的なことはないのか、など気になる点があるのでそれについてまとめて行きます。

ロジックについて

clustermap ではクラスタリングをすべて scipy.cluster.hierarchy.linkage にまかしているという記述があります。実際 clustermap 関数を呼び出すと

Cluster Class インスタンスが新しく生成され、インスタンスの plot メソッドが呼ばれる
plot 内部で self.plot_dendgram が呼ばれる
self.dendgram では dendgram method が呼ばれ内部で _DendrogramPlotter インスタンスが新しく生成され、インスタンスの plot が呼び出される
Dendgram.plot で scipy.cluster.hierarchy.linkage によって linkage が生成される

という流れで処理が走ります。というわけでまずは scipy の linkage を理解する必要が有ることがわかりました。

Scipy.cluster.hierarchy.linkage

linkage は階層型クラスタリングを行う関数です。

Scipy.cluster.hierarchy.linkage API scipy.cluster.hierarchy.linkage — SciPy v1.1.0 Reference Guide

具体的には特定の指標のベクトル $y$ を入力としてその hierarchy linkage を返します。階層型クラスタリングとはすべての点が集まった状態を頂点として各点がひとつのクラスタになった状態を枝とするような木構造で表現できるクラスタリングのことです。階層型ではないクラスタリングで有名なのは k-means です。 k-means はある点が特定のクラスタに属するという状態が出力なためクラスタ同士に階層がありません。

入力値

一次元の距離尺度ベクトル、若しくは二次元の shape = (クラスタにしたい要素数, クラスタの特徴ベクトル) という形状の配列を指定します。

一次元ベクトルを渡す場合は、クラスタにしたい要素同士 $n$ のおのおのの距離が入った配列を指定する必要があります。そのため長さは必ず $nC_2$ である必要があります。

返り値

返り値は shape = (n-1, 4) の形状の matrix $Z$ です。
$Z$ の第 $i$ 番目の行ベクトルは $i$ 番目のクラスタリングの結果が入っています。

仮に $i$ 番目の行ベクトルを $v$ とします。この時 $v[0]$ と $v[1]$ は新しい $n+i$ 番目のクラスタとして結合される要素の index を表しています。また $v[2]$ には結合されたクラスタ $v[0], v[1]$ の距離が、 $v[3]$ には結合後のクラスタの要素数がそれぞれ格納されています。

クラスタリングの指定

クラスタリングをどのように実行するか、を制御することができます。これはクラスタリングをする際に何を決めなくてはならないか、を考えるとわかりやすいです。

第一にクラスタリングする際にはクラスタごとの距離を計算する必要があります。これはアルゴリズムが

今存在しているクラスタ同士の距離をすべて計算し
そのなかでもっとも近い物同士を結びつける (linkage)
上記を繰り返す

というふうに進んでいく為 step1 でクラスタ間の距離計算を行う必要があるためです。

このクラスタごとの距離の計算を行う関数は「クラスタ化を考えているふたつの集合 $Y, Y'$ の中に存在する2つの要素 $u, v \in Y, Y'$ を入力としてその近さを返す距離尺度 $d: Y \times Y' \to \mathbb{R}$ 」である必要があります。

scipy にはいくつかその関数 (引数としては method で指定します) が用意されていますが、初めは単純な single を使います.
single は以下の数式で表される指標で, クラスタ内の要素の組み合わせすべての中で距離の最小値を返すものです

$$ d(u, v) = \min_{a \in u, b \in v}\left( {\rm dist}(a, b) \right) $$

ここで ${\rm dist}$ は2つのクラスタの要素を与えられた時に実数値を返す関数です. もし入力 y として1次元配列が渡された時は単に絶対値を返す関数となります。一方で二次元配列 (n, m) が渡された時は m 次元ベクトル二点を入力としてその距離を返す関数 ${\mathbb R}^m \times {\mathbb R}^m \to {\mathbb R}$ を指定する必要があります。(scipy では metrics で指定します)

例

from scipy.cluster.hierarchy import linkage

y = [2, 8, 0, 4, 1, 9, 1, 0]

# y を特徴ベクトルとしたいので shape = (8, 1) に変換する
x = [[d] for d in y]
z = linkage(x, method='single', metric='euclid')

この場合だと dist はユークリッド距離になります。各要素の特徴次元が一次元の整数値なのでまあ大体の metric を使っても結果は変わりません。例えばチェビシェフ距離とかでも出力結果は一緒です。

>>> z_abs = linkage(x, method='single', metric='chebyshev')
>>> z_abs == z

    array([[ True,  True,  True,  True],
           [ True,  True,  True,  True],
           [ True,  True,  True,  True],
           [ True,  True,  True,  True],
           [ True,  True,  True,  True],
           [ True,  True,  True,  True],
           [ True,  True,  True,  True]])

つぎにこの出力値を解釈していきます。

>>> z

    array([[ 4.,  6.,  0.,  2.],
           [ 2.,  7.,  0.,  2.],
           [ 0.,  8.,  1.,  3.],
           [ 9., 10.,  1.,  5.],
           [ 1.,  5.,  1.,  2.],
           [ 3., 11.,  2.,  6.],
           [12., 13.,  4.,  8.]])

まず初めの行について考えてみます。

>>> z[0]

array([4., 6., 0., 2.])

index 0, 1 の値を見ると 4 番目と 6 番目の要素を結合していることがわかります(値はともに 1 です). それらの距離は 0 となっています. 要素がともに同じ値であるので明らかです。そしてこれらの要素は $8 + 0 = 8$ 番目のクラスタに割り当てられました。

>>> z[2]

array([0., 8., 1., 3.])

つぎに第2行目をみてみます。ここではクラスタ 0, 8 を結合しています。クラスタ0 は即ち第0番めの要素でこれは 2 です。一方クラスタ8は8番目の要素(すなわち第1行目で出来たクラスタ)を指しているのでこれらの値はどっちも1でした。

2 と (1, 1,) のユークリッド距離の最小値は 1 なので距離は1です。そしてまとめられたクラスタは要素数3になり, 8 + 2 = 10 番目のクラスタに割り当てられました。

こんな感じにもっとも距離の近いクラスタを集結させていくのが linkage で行われている hierarchical/agglomerative clusteringというものです。

method の種類

method は"single" 以外にもいくつかの種類が用意されています.

https://docs.scipy.org/doc/scipy/reference/generated/scipy.cluster.hierarchy.linkage.html

single や complete といった最小値、最大値を取るものは特徴の中に一つでも近い（遠い）ものがあるときに極端なクラスタを作りがちなのでノイズや変数間のスケールに左右されてしまいます。一般には ward 法が外れ値やスケールに堅牢であるとされているようです。¹

Seaborn.clustermap

scipy の linkage の理解が出来たところで seaborn.clustermap の方に戻りましょう. 主な引数は以下のようになっています.

基本

data: pandas.DataFrame
method: default は "average" . linkage のクラスタ間の距離尺度を変えたい時はこの値を変更します。scipy.cluster.hierarchy.linkage の method と役割は同じです。
metric: default は "euclidien". 要素間の距離尺度を変えたいときはこの値を変更します。 scipy.cluster.hierarchy.linkage と役割は同じです。例えば予測値同士の相関に関してクラスタにしてほしいなーという時は metric="correlation" とかにすると相関ごとにクラスタにしてくれるので良い様な気がします。
z_score: 数値が代入されるとその軸方向で平均 0 分散 1 に正規化します。ずなわち 0 の時が行の方向で 1 の時が列方向です。行方向に正規化するのは画像データとかが該当するでしょうか(各画像ごとに平均ゼロ分散1に揃えたい)。普通の集計データの時は列方向を使うことが多いと思います（列方向に正規化すると各列の値がどれだけ平均からずれているかという無次元情報に変換されるため、特徴ごとのスケールなどを考慮しなくて済むからです）。
standard_scale: 数値が代入されるとその軸方向を $[0, 1]$ の範囲に圧縮(拡大)します。分散を1にしないスケーリングです。

ちょっとテクいことをする時

{row,col}_linkage: 行(列)の linkage を指定できます。デフォルトの挙動では行と列に同じ method 及び metric での linkage を行います。違うロジックを使いたいーという時には行の linkage, 列の linkage を予め scipy.cluster.hierarchy.linkage で計算しその結果を渡すとそのクラスタで linkage グラフを描写してくれます。

では実際にいろいろ試してみます。まずは average method でクラスタリングしてみます。

g = sns.clustermap(df_iris, method='average', cmap='viridis')
g.ax_col_dendrogram.set_title('Average Euclidean')
g.savefig('average_euclid.png', dpi=150)

f:id:dette:20181119030411p:plain

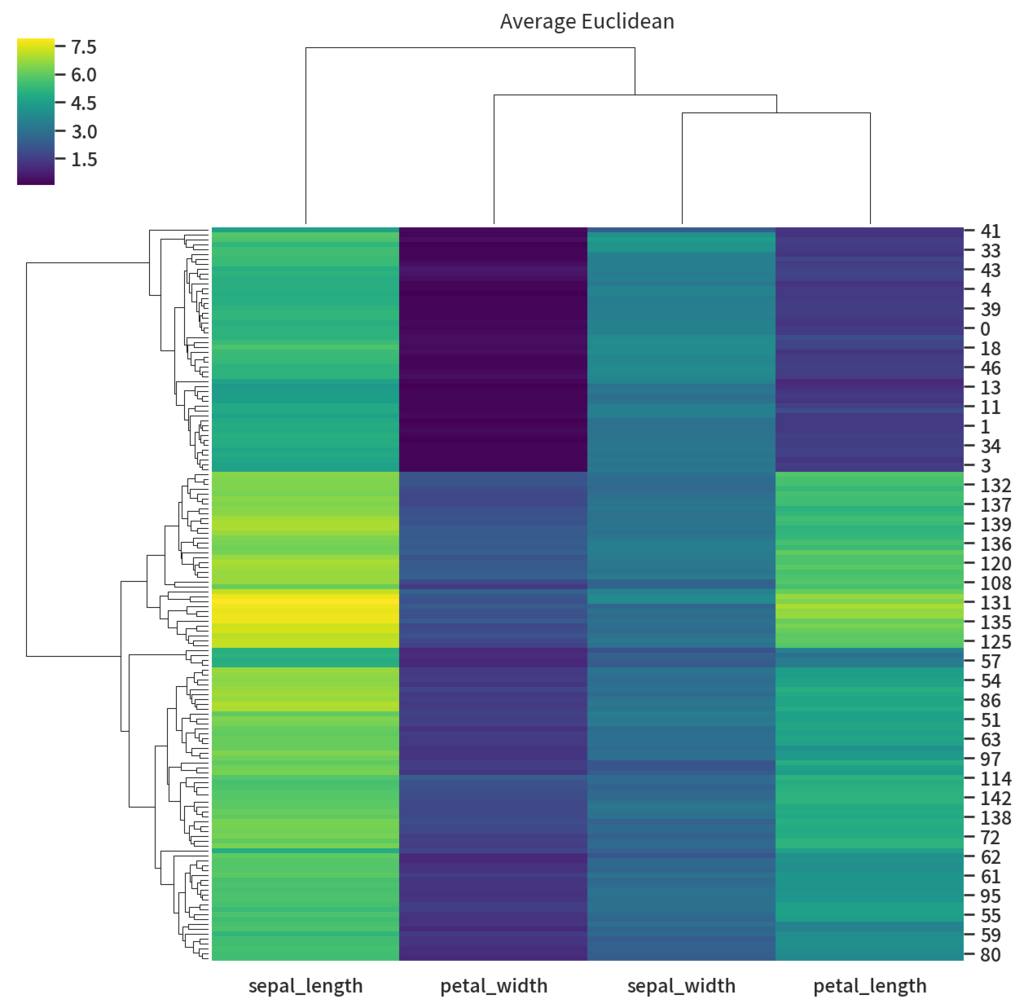
これでもいいんですが少し列間の類似度に差があまり無いように表示されています。これは列に対してユークリッド距離で距離を測っていてかつ正規化などをしていない為に列の値の平均値のズレに引っ張られている為です。ちょっといたずらで petal_witdh の行に 100足してみましょう

df_fix = df_iris.copy()
df_fix['petal_width'] += 100
g = sns.clustermap(df_fix, method='average', cmap='viridis')
g.ax_col_dendrogram.set_title('Average Euclidean')
g.savefig('fixed_average_euclid.png', dpi=150)

f:id:dette:20181119031140p:plain

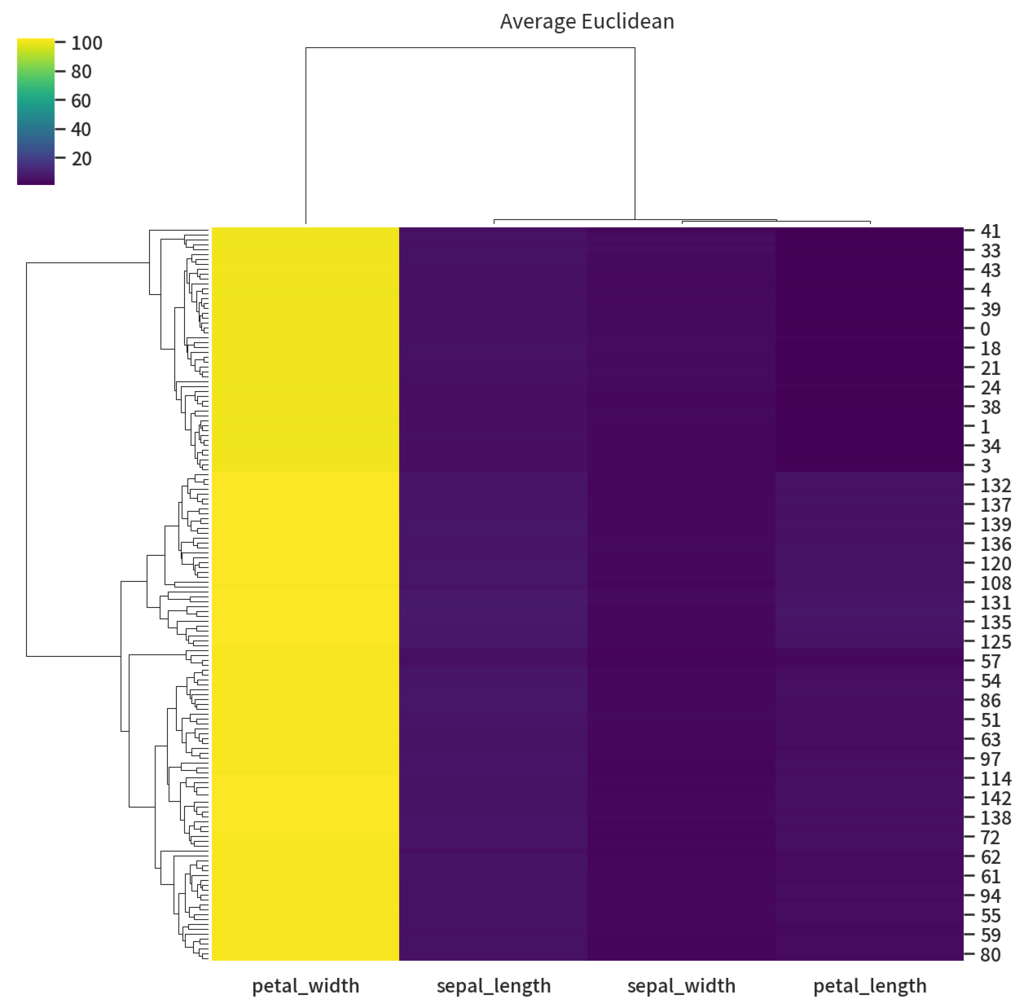
petal_width だけ仲間はずれになってしまいました。これはユークリッド距離を使っているために元データと比べ列比較の際に各要素の差分が 100 増えたことが原因です。

では次は距離をユークリッド距離ではなく相関係数にしましょう。相関係数の式はその系列の平均で引いた後に要素ごとに積を行うので平均を 100 増やしても問題ないはずです。

g = sns.clustermap(df_fix, method='average', metric='correlation', cmap='viridis')
g.ax_col_dendrogram.set_title('Average Correlation')
g.savefig('fixed_average_correlation.png', dpi=150)

f:id:dette:20181119031759p:plain

列のクラスタはいい感じになりました! でもちょっと色が意味をなしていないですね。というわけで今度は列方向に正規化します。

g = sns.clustermap(df_fix, method='average', metric='correlation', z_score=1, cmap='viridis')
g.ax_col_dendrogram.set_title('Average Correlation')
g.savefig('fixed_and_normalized_average_correlation.png', dpi=150)

f:id:dette:20181119031820p:plain

だいぶ見栄えも良くなりました。ちょっとあれな点があるとすると行方向にも相関を使っている所が微妙かも知れません。というわけで行にはコサイン類似度を使ってクラスタリングをやるようにしてみます。

# 列方向は相関で
col_link = linkage(df_iris.values.T, method='average', metric='correlation')

# 行方向はユークリッド距離でクラスタ化
z = (df_fix.values - df_fix.values.mean(axis=0)) / df_fix.values.std()
row_link = linkage(z, method='ward', metric='euclidean')
g = sns.clustermap(df_fix, col_linkage=col_link, row_linkage=row_link, z_score=1, cmap='viridis')

g.ax_col_dendrogram.set_title('Average-Corr  Ward-Euclidiean')
g.savefig('average-corr__ward-euclidean.png', dpi=150)

f:id:dette:20181119032923p:plain

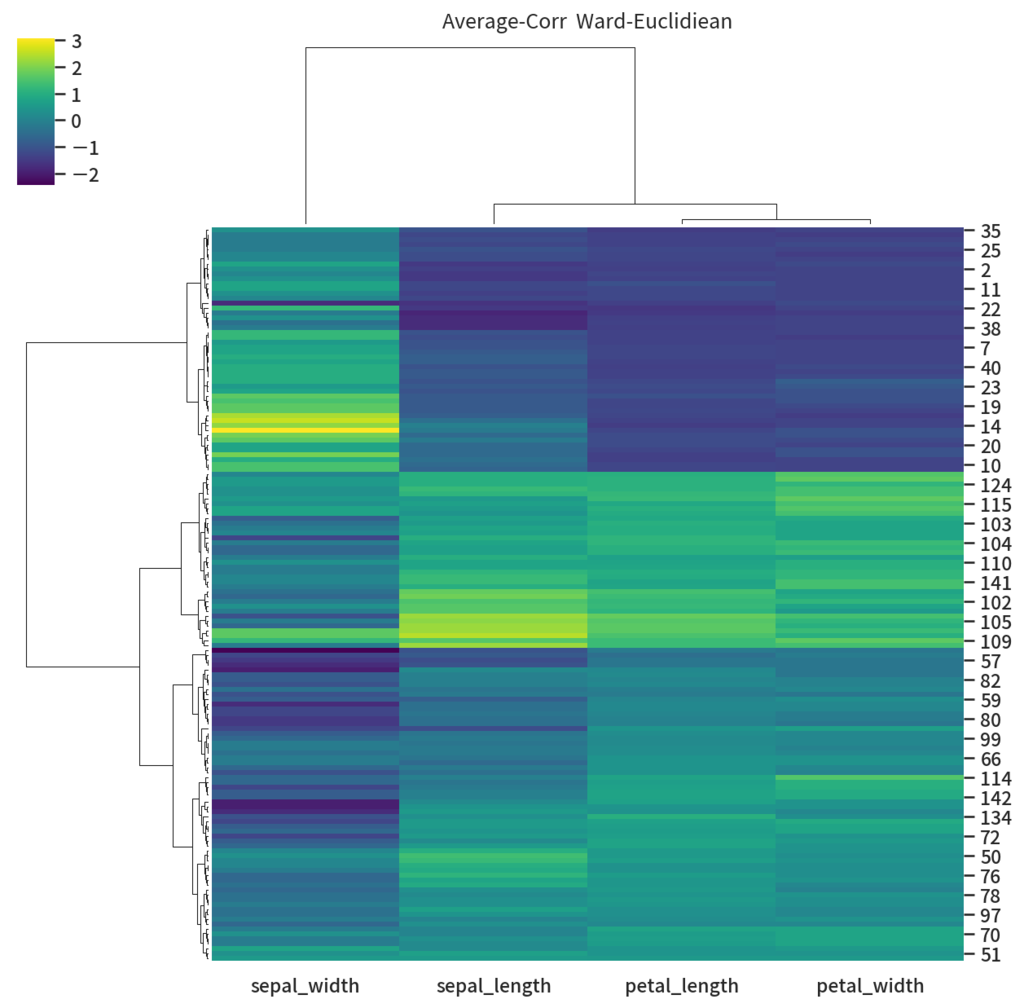
先よりは sepal_width の右上あたりに3あたりを取るクラスタっぽいものができるようになりました。

気をつけたほうが良さそうなこと

以上色々と試してきましたが、実際に可視化をする際に気をつけたほうが良さそうなポイントについて考えてみます。

scaling

今回の iris のような基本的なテーブルデータでは列ごとに意味を持っている場合が多いです。

そのためスケーリングを行うとするならば列方向の指定, 即ち z_score=1 や standard_scale=1 を指定するのが良さそうです。
また初めからスケーリングしてしまうと列ごとの値の大小がわからなくなってしまうため、列ごとの大きさの情報がわかっていない場合はスケーリングせずプロットしてみる、というのもありかも知れません。

アルゴリズムの選定

metric については列に対してはユークリッド距離ではなく相関係数を使ったほうが良いでしょう。ユークリッド距離を使うのであれば、列ごとのスケーリングもしくは平均値を均すような前処理を行うべきです。

method については色々と試してみましたが metric さえちゃんと選んでいれば average や ward など選んでおけば大体事足りそうです。² 一方で "single" や "double" のような最小値/最大値しか見ないロジックを指定すると出力結果が極端になりがちな印象を受けました。のでちょっといつ使ったらいいのかなーという気分です。

またテーブルデータでは列方向には相関 correlation を使いたい場面が多いと思いますが行方向 (レコードごとの距離測定) にも相関でいいのか？という純粋な疑問があります。³ なのでちょっと面倒ですが時間が有る場合は自分で linkage を計算してやるのがよいように思えます。

http://ibisforest.org/index.php?Ward%E6%B3%95 がわかり易すぎるので自分の努力要らなかった説))↩
ward を指定する際には metric は "euclidean" にする必要があります↩
このあたりは SVM などデータ点どうしの距離を使うモデルでの前処理でも問題になるところだと思うのですが、未だに何がいいのかよくわかっていません。ノリで列方向に正規化したりはしていますが…↩

2018-11-03

重みのスケールに依存しないSGD: Path Normalized Optimization in Deep Neural Network

論文機械学習 SGD

表題の論文を読んだのでまとめます！

url: [1506.02617] Path-SGD: Path-Normalized Optimization in Deep Neural Networks

Path-SGD を考えたモチベーション

ニューラルネットワークがこの論文の主題です。

Rescaling

今、あるニューラルネットワークの $i, i+1$ 番目の隠れ層の重み $W_i, W_{i+1}$ を取り出して $i$ 番目の重みを $x$ 倍して $i+1$ 番目の重みを $1/x$ 倍する操作を考えてみます(バイアスの大きさは 0 とします)。$i$ 層の出力を $y_i$ 入力を $z_i$ と表すことにします。隠れ層での計算は入力に対し重みを行列積することで表現できますから上記の操作後の隠れ層での出力を $\hat{y}_i$ とすると

$$ \begin{aligned} y_{i+1} &= W_{i+1} \cdot y_{i} = W_{i+1} \cdot W_i \cdot z_{i} \\ \hat{y}_{i+1} &= \frac{1}{x} W_{i+1} \cdot \hat{y}_i = \frac{1}{x} W_{i+1} \cdot (Wx) \cdot z_{i} \\ &= \frac{1}{x} \times x W_{i+1} \cdot W_i \cdot z_i \\ &= y_{i+1} \end{aligned} $$

となり出力は変化しません。このような重みに対する操作を rescaling と呼ぶことにします。

勾配法の Scaling への弱さ

ニューラルネットワークの学習では、勾配法の近似である確率的勾配法 (Stochastic Gradient Descent) が使われ、勾配計算には Forward Backward が用いられます。この時重みへの正則化としてL2正則化を考えて少し重みをゼロに近づけるような効果を持たせて SGD を使うことが多いです。この正則化は WeightDecay と呼ばれることもあります。

さてこの確率的勾配法、ひいては勾配法はネットワークの rescaling に対して不変ではありません。これは勾配法の重み更新で使う Forward/Backward の勾配が、関連するレイヤーの重みスケールに依存しているからです。

そのため勾配法をネットワークの各層の重みが違うスケールをもっている Unbalanced な場合に使うと、学習は上手く進みません。以下のグラフはスケールがそろっているときと揃っていないときのロス関数値をプロットしたものです。

f:id:dette:20181103194415p:plain

以下の図はSGDでの重み更新の具体です。左のネットワークではすべての重みのスケールが 1~10 程度なので調度良く値が更新されています。一方で右の例では10~100 のものと 0.1 のものが混合しています。そのため勾配更新を行うと大きい値の物はほぼ変わらず、小さい値の重みが一気に更新されてしまっています。

f:id:dette:20181103194746p:plain

「じゃあ重みが歪んでいる時でもいい感じに更新する最適化方法無いの？」という疑問に応えるのが、この論文の趣旨になっています。それが表題にもある Path-SGD です。*1

準備

考えるのは $d$ 層のニューラルネットワークです。活性化関数は RELU とします。このネットワークをDAG $G(V,E)$ として表現します。ここで $V$ はノードを表し $E$ はエッジを表しています。 $D, C \in \mathbb{N}$ を入力, 出力の次元数とします。即ち入力ノードは

$$ v_{in[1]}, \ldots, v_{in[D]} \in V $$

と表現できます。

一般的な正則化

はじめに、ネットワークの各レイヤーの重みごとにグルーピングされた正則化を考えていきます。パラメータ $p \ge 1, q \le \infty$ を用いて一般的な正則化関数は以下のように表現できます。

$$ \mu_{p,q}(w) = \left( \sum_{v \in V} \left( \sum_{(u \to v) \in E} | w_{u \to v} |^p \right)^{q/p} \right)^{1/q} $$

各ノードごとの足し算の項 $\sum_{v \in V}$ が有るためこれはグルーピングされた正則化関数の一般化であることがわかります。簡単な例であると $p = q = 1$ の時は L1 正則化に $p = q = 2$ の時にL2正則化(Weight Decay)に対応します。

これら以外にも重みの最大値を正則化とする max-normalization というものがあります。これは上記の一般形式で $q \to \infty$ を考えた時の値として表現できます。

$$ \mu_{p,\infty}(w) = \sup_{v \in V} \left( \sum_{(u \to v) \in E} | w_{u \to v} |^p \right)^{1/p} $$

重み不変な正則化

重み不変な正則化とは、重みに対して rescaling の操作を行った時に値が変わらない正則化関数を指しています。

max-normalization は重みの上限をとっているためこれは明らかに重み不変性を満たしていません。適当なノードの入力を小さくして出力を大きくすれば、いくらでも上限値を大きくすることができるからです。

ここで、もし多数のネットワークが重み不変、すなわち入力が同じなら出力も同じである、という性質を満たしていて、どれでも好きなものを選べると仮定しましょう。どれでも出力が同じなら、そのなかでもっとも正則化関数の値が小さいものを選ぶことが望ましいはずです。

現実には重み不変を持つネットワーク全てに対して正則化を考えることは難しいですが、ラッキーなことに max-normalization の場合この最小値を計算することが出来ます。それが以下の path-normalization です。

$$ \phi_p(w) = | \pi(w) |_p = \left( \sum_{v_{in}[i] \to \cdots v_{out}[j]} \left| \prod_{k=1}^d w_{e_k} \right|^p \right)^{1/p} $$

ここで $\pi(w) \in \mathbb{R}^N$ はパスベクトルと呼び、次元数 $N$ は入力から出力までのパスの組み合わせ数です。上記の式中では $v_{in}[i] \to \cdots v_{out}[j]$ と表されている部分が組み合わせ数に対応しています。この式もやや込み入っていますが、入力 $i$ と出力 $j$ を色々と入れ替えた時にできるすべてのパス、を表しているのでパスの組み合わせに相当していることが解ると思います。

パスベクトルの各次元の値はそのパス上の重みをすべて積算したものになっています。そしてパスベクトルの $p$ ノルムが $\phi_p$ です。ちょっとややこしいですね。

ややこしいものを持ちだしたのには理由があって、実はこの $\phi_p$ は max-normalization との間に以下のような面白い性質を持ちます。

$$ \phi_p(w) = \min_{\tilde{w} \sim w} \left( \mu_{p, \infty}(\tilde{{w}}) \right)^d $$

ここで $\tilde{w} \sim w$ で表される $\tilde{w}$ は $w$ を rescaling した中で任意の入力に対して出力が $w$ と同じになるという同値類です。

これは即ち path-normalization $\phi_p(w)$ の値は rescaling な重みの中での max-normalization の最小値であることを表しています。ということは path-normalization を最小化すれば勝手に max-normalization の最小値も下がるということがわかります。しかもその値は rescaling を許したすべての max-normalization の値の中でもっとも小さいのです。これは嬉しい。

また明らかに任意の $w \sim \tilde{w}$ に対して $\phi_p(w) \sim \phi_p(\tilde{w})$ であるので、これより path-normalization は重み不変性を持っていることがわかります。

以上から path-normalization は

max-normalization の最小値であること
重み不変であること

という良い正則化項であることがわかりました。

Path-Normalization を持つ SGD

では path-normalization を正則化項とするような目的関数を考え、これに対して勾配法を考えていきます。この時すべての重みを厳密に最適化することが難しいので、特定のエッジの重み $w_e$ のみを更新することを考えます。

今第 $t$ ステップの重み $w^{(t)}$ を得ていて $t+1$ での $e$ の重み $\hat{w}_{e}^{t+1}$ を計算する場面を考えます。ロス関数を $L$ として偏微分すると以下の式を得ます。

$$ \hat{w}_{e}^{t+1} = w_{e}^t - \frac{\eta}{\gamma_p(w^{(t)}, e)} \frac{\partial L}{\partial w}(w^{(t)}) $$

ここで $\gamma $ は以下の式で表される重みの積になります。

$$ \gamma_p (w, e) = \left( \sum_{v_{in}[i] \cdots \overset{e}{\to} \cdots v_{out}[j]} \prod_{e_k \ne e} | w_{e_k} |^p \right)^{2/p} $$

これは入力から出力への経路のうちで $e$ の重みだけを含まない $\pi(w)$ のノルムになっています。このことから例えば $e$ に対応する重みがとても大きい値を持っていると仮定すると $\gamma$ の値はその値が除外されるため小さくなり、勾配に係る係数は大きくなります。反対に小さい時には $\gamma$ は大きくなり勾配に係る係数は小さくなります。

結果として自分の大きさに応じた勾配更新が行われるようになることがわかります。これは通常のSGDでは得られなかった性質です。（前半のレイヤーごとに重みが違う場合の更新を考えてみるとわかりやすいと思います）

このことを数学的に行ったのが Theorem4.1 でこのPath-SGDの更新はスケールに対して不変であることが示されています。

じっけん

有名データセットを用いて数値実験を行っています。比較するのは Path-SGD を Unbalanced な条件で学習させたものと SGD/AdaGrad を Unbalanced/Balanced な条件で学習させたものです。

f:id:dette:20181103194205p:plain

まず SGD を Unbalanced で実行すると MNIST ですら学習できていないことがわかります。 AdaGrad はもうちょっとがんばっていますがやはり苦しそうです。一方で Path-SGD では Unbalanced にもかかわらず学習が上手く進み、また Balanced の場合の AdaGrad と並ぶかむしろそれよりも学習が早いことがわかります。*2

まとめ

Unbalanced な重みでは SGD は機能しない。それは勾配法が重み不変性をもたないから
Path-Normalization は max-normalization の最小値であり、重み不変。
それを正則化項として持つ objective を考えた path-SGD も重み不変。故に重みが Unbalanced でも学習が進む。

感想

重み不変性という観点が純粋に面白かった。また max-normalization の重み不変空間上での最小値が path-normalization の値につながっているのも綺麗。

一方でそもそも重みのスケールが異なるようなネットワークって存在する時あるんだろうか (転移学習とかならありうる?) とか数値実験で目的関数違うやつを同じグラフにプロットするのはどうなの（せめて精度とかにして欲しかった）とか思ったり。

気になった点としては、やはり重みごとにその勾配に対する係数を保存しないとだめだという点 ($\gamma_e$ の所)。著者は効率的な実装方法があるよーと述べていて forward backward 方式で1回計算すればいいように済ませる実装方法を提案しているがそれだとしても毎回の更新時に重みの係数も更新するのは面倒だし、重みが増えてくるとメモリ的にもしんどそう（とはいえたかだか二倍程度だからしれているのか?)。自分で実装してみたいなと思った時もこの面倒さがボトルネックでまだ出来ていません。Adam とか他の適合的なアルゴリズムが楽すぎるってことなのかな…

*1:pathという言葉がでている理由も導出を見ていると解ると思います

*2:そもそも正則化項が違うため最適解も最適値も違っているので training loss にはあまり意味は無いかも知れませんが……

2018-10-20

Boid Model による ALife の実装 with Javascript

Alife JavaScript Nuxt Vue

計算機状で生命体を模したモデルを作り、その挙動を研究するという分野があり、一般に人工生命 (Alife) と呼ばれています。その中でも「群れ」をモデル化したものに boid model と呼ばれるものがあります。

今回は Boid Model の簡単な説明とそれを Javascipt + vue.js を使ってブラウザ上でインタラクティブにあそべるところまでを実装していきます。

完成図

agitated-goldberg-260b08.netlify.com f:id:dette:20181020175739g:plain

Boid Model とは

Boid Model とは Craig Reynolds によって開発された群れを模した Alfie のモデルのことを指します。Boid とは「bird-oid object」の省略系で、このモデルが鳥を模したものであることが名前からもわかります。

Boid は以下の3つの基準にしたがって行動します。

1. 分離

f:id:dette:20181020164507p:plain

自分の周りに沢山鳥がいると飛びづらいですよね。なので boid は自分の近くの boid から離れようとします。これが分離の動きです。

2. 平均化

f:id:dette:20181020164540p:plain

boid は周りの動きに敏感です。自分の近くにいる集団の速度と自分の速度を一致させようとします。これが平均化の動きです。

3. 結束

f:id:dette:20181020164600p:plain

boid は周りの boid から完全に離れることは望んでいません。ですので boid はまわりの boid の重心座標へ移動しようとします。これが結束の動きです。

基礎的な boid は以上の3つのルールにしたがって行動します。

一見単純な用に見えますが、これらの重み付けを変えたり、 boid が見える周りの範囲の大きさを変えたりすることで、多種多様な動きをするようになります。

実装

今回は boid モデルを javascript で実装します。

まず boid を扱う際には物理モデルを作成する必要があります。ここでいう物理モデルは座標 $x$ 速度 $v$ 加速度 $\alpha$ を物体は持っていて以下の式によって変化する、ということを指します。

$$ \dot{x}(t) = v(t) \\ \dot{v}(t) = \alpha(t) $$

実際にコンピューター上ではこれを離散化する必要があるため、ある短い時間 $\Delta t$ を用いて以下のように近似してやります。

$$ x(t+1) = x(t) + \Delta t v(t) \\ v(t+1) = v(t) + \Delta t \alpha(t) $$

必要な数式はこれだけです。（たぶん）

下準備

では実装に入ります。まず大量に座標を扱うことになるので、座標系クラス Coodinate を作ります。とりあえずは二次元で考えるので変数は x, y の２つにしておきます。ここでは省略しましたが座標同士の足し算、引き算、掛け算、ノルム計算などを実装しました。

class Coodinate {
  constructor(x, y) {
    this.x = x
    this.y = y
  }

  /**
   * 座標に数値を掛け算した座標を返します
   *
   * @static
   * @param {Coodinate} a
   * @param {Number} x
   * @memberof Coodinate
   */
  static mult(a, x) {
    const retval = new Coodinate(a.x * x, a.y * x)
    return retval
  }
  // などなど
}

次に物理法則にしたがって動く物体の基本となるクラス AbstractObject を作ります。このオブジェクトは場所、速度、加速度、速度の最大値、自分の位置の履歴を管理します。

class AbstractObject {
  /**
   *Creates an instance of AbstractObject.
   * @param {Coodinate} initPosition
   * @param {Numbe} maxVerocity オブジェクトの最大速度
   * @memberof AbstractObject
   */
  constructor(initPosition, maxVerocity = 5) {
    this.position = initPosition
    this.verocity = new Coodinate(Math.random(), Math.random())
    this.acceleration = new Coodinate(0, 0)
    this.maxVerocity = maxVerocity
    this.history = []
    this.ratio = null
  }

  /**
   * 加速度を元に座標と速度を更新するメソッドです
   *
   * @param {Coodinate} newAcceleration
   * @memberof AbstractObject
   */
  update(newAcceleration) {
    this.acceleration = newAcceleration
    this.verocity.plus(this.acceleration)
    const vNorm = Coodinate.distance(this.verocity, new Coodinate(0, 0))
    this.ratio = vNorm

    if (this.maxVerocity < vNorm) {
      const ratio = this.maxVerocity / vNorm
      this.verocity = this.verocity.multBy(ratio)
    }
    this.position.plus(this.verocity)

    this.history.push(Coodinate.copy(this.position))
  }
}

物体の位置が更新されるときは加速度を元に速度、速度を元に位置、というふうに計算していくので、加速度を渡して位置情報を update する関数を用意しています。

次に実際に動く boid object を作ります。今回は Fish と名づけました(今になって bird のほうが適切だったと気づきましたがまあ魚も群れを作るので）

/**
 * 魚の boid model
 *
 * @class Fish
 * @extends {AbstractObject}
 */
class Fish extends AbstractObject {
  static maxAccelerationNorm = 0.1
  static meanForceRatio = 0.7
  static dislikeForceRatio = 5.0
  static counter = 0

  /**
   * 魚のインスタンスを作成します
   * @param {Coodinate} initPosition
   * @param {number} [sakuteki=100] 魚が見える範囲です。この範囲内の魚に対して boid の3原則を適用します
   * @param {number} [dislikeDistance=20] この範囲内の魚からは遠ざかる動きをします.
   * @memberof Fish
   */
  constructor(initPosition, sakuteki = 100, dislikeDistance = 20) {
    super(initPosition)
    this.sakuteki = sakuteki
    this.dislikeDistance = dislikeDistance
    Fish.counter += 1
    this.id = Fish.counter
  }
  /**
   * 次のフレームでの自分の加速度(意志)を決定します
   *
   * @param {[Fish]} nearlyFishes
   * @memberof Fish
   */
  nextAcceleration(nearlyFishes) {
    // 近くに魚が居ない時加速しません
    if (nearlyFishes.length === 0) return new Coodinate(0, 0)

    const vList = nearlyFishes.map(f => f.verocity)
    const vMean = Coodinate.mean(vList)
    const pMean = Coodinate.mean(nearlyFishes.map(f => f.position))

    // 速度の平均値にどれぐらい合わせるかを計算 (法則2)
    const vDirection = Coodinate.minus(vMean, this.verocity)
      .norm()
      .multBy(Fish.meanForceRatio)

    // 中心に移動するちからのベクトルを計算 (法則3)
    const pDirection = Coodinate.minus(pMean, this.position).norm()

    let direction = pDirection.plus(vDirection)

    // 近すぎるおさかな
    const tooNearFishPositions = filterByDistance(
      nearlyFishes,
      this.position,
      this.dislikeDistance
    )

    if (tooNearFishPositions.length > 0) {
      const tooNearMeanPos = Coodinate.mean(
        tooNearFishPositions.map(f => f.position)
      )
      // 近すぎる魚からどのぐらい離れるかのベクトルを計算(法則1)
      const tooNearDirection = Coodinate.minus(tooNearMeanPos, this.position)
        .norm()
        .multBy(Fish.dislikeForceRatio)
      direction.minus(tooNearDirection)
    }

    return Coodinate.normalize(direction).multBy(Fish.maxAccelerationNorm)
  }
}

constructor に sakuteki と dislikeDistance のパラメータが加わりました。

sakuteki
- 自分の周りのこの範囲の魚を見ることができます。先の boid 3法則はこの範囲内の魚に対して適用されます。
dislikeDistance
- boid の第一法則である分離に関するパラメータです。この範囲内にいる魚からは逃げようとする動きを取ります。(コメント中の近すぎるお魚がそれに相当します。)

距離で絞り込んでくる必要がでたので関数を一つ用意しました。 viewFrom からみて maxDistance 内にいる魚を返す関数です。

function filterByDistance(fishes, viewFrom, maxDistance) {
  return fishes.filter(fish => {
    const d = Coodinate.distance(fish.position, viewFrom)
    return d < maxDistance
  })
}

最後に魚を泳がせるフィールドを用意します。

/**
 * 魚を泳がせるフィールドクラス
 *
 * @class Field
 */
export class Field {
  /**
   *Creates an instance of Field.
   * @param {number} [width=1000] フィールドの横幅
   * @param {number} [height=500] フィールドの縦幅
   * @param {number} [sakutekiRange=200] 新しく作る魚がどれぐらいの範囲を見れるか
   * @param {number} [dislikeDistance=20] 新しく作る魚はこの範囲以下の魚から離れようとします。
   * @memberof Field
   */
  constructor(
    width = 1000,
    height = 500,
    sakutekiRange = 200,
    dislikeDistance = 20
  ) {
    this.width = width
    this.height = height
    this.fishes = []
    this.newFishes = []
    this.sakutekiRange = sakutekiRange
    this.dislikeDistance = dislikeDistance
    this.isUpdating = false
  }

  /**
   *ランダムな位置に魚を追加します
   *
   * @memberof Field
   */
  addFish() {
    const x = (this.width * (0.5 + Math.random())) / 2
    const y = (this.height * (0.5 + Math.random())) / 2
    const pos = new Coodinate(x, y)
    const newFish = new Fish(pos, this.sakutekiRange, this.dislikeDistance)
    this.newFishes.push(newFish)

    if (this.isUpdating) return
    this.fishes = this.fishes.concat(this.newFishes)
    this.newFishes = []
  }

  /**
   * フィールドの時間を一つ進めます
   *
   * @memberof Field
   */
  next() {
    this.fishes = this.fishes.concat(this.newFishes.slice())
    this.newFishes = []

    // 初めに魚全員の行動(加速度)を決定する
    const accelerations = this.fishes.map(fish => {
      const fishesCanView = filterByDistance(
        this.fishes.filter(f => f !== fish),
        fish.position,
        fish.sakuteki
      )
      return fish.nextAcceleration(fishesCanView)
    })

    // 決めた行動（加速度）にしたがって更新
    this.fishes.forEach((fish, idx) => {
      const acc = accelerations[idx]

      // フィールドから外に出ようとする魚に対しては強制的に元に戻るような加速度をつける
      if (fish.position.x > this.width) {
        acc.plus(new Coodinate(-1, 0))
      }
      if (fish.position.x < 0) {
        acc.plus(new Coodinate(1, 0))
      }

      if (fish.position.y > this.height) {
        acc.plus(new Coodinate(0, -1))
      }
      if (fish.position.y < 0) {
        acc.plus(new Coodinate(0, 1))
      }

      fish.update(accelerations[idx])
    })
  }
}

動き自体は Fish が担っているので Field では特定の Fish インスタンスがどの範囲が見えているのか（見えている魚の集合はなんなのか）の計算が主になっています。

あとはこれを vue.js 上でレンダリングすると完成です。要は

FIeld のインスタンス field を作成
window.setInterval で定期的に field.next() を呼び出す

を繰り返せば OK です。

実装: https://github.com/nyk510/boid-model/blob/master/components/boid/BoidCanvas.vue *1

Deploy

今回は netlify を使って nuxt を静的ファイルとしてデプロイしました。

agitated-goldberg-260b08.netlify.com

パラメータ変えて遊んでみると、いろいろな周期と規則が見えてきて面白いです。

今回は本当にさわりだけでしたが、面白い！と思った人は Alife とか boid で検索して本とか論文とか読んで僕に教えてくれると嬉しいです;)

*1:vueファイルの解説も書きたかったですが、あまりにも長いので断念