matplotlibで高校生っぽいグラフを描く

高校の時によくみたグラフをmatplotlibで書いてみたくなったので、やってみました。

練習として初めてデコレーターを使って、プロットしたオブジェクトをいじって軸をあれこれするようにしてみました。
機能としてあるのは知っていたのですが、使ってみるとデコレーターって意外と便利ですね。やっぱり食わず嫌いは良くないなと思いました。

作れる画像はこんな感じです。

意外と苦労するのが軸の矢印を作るところで、画像の縦横比が変わった時にもちゃんと特定の比率の長方形に頂点を持つ矢印を持つようにしてあります。さっくり適当なグラフを書くのには使えるかも。

DCGANをChainerで実装

DCGANとは

DCGANはランダムなベクトルから画像を生成するGeneratorと、画像が与えられた時にその画像がGeneratorによって作られたものなのか、本当の画像なのかを判定する関数Discriminatorでなりたっています。

DCGANのアイディア

この2つの関数を相互に競わせるように更新することで、画像を生成するGeneratorをもっともらしいものへと更新します。

Generatorは、できるだけDiscriminatorに偽物だと判定されないように、重みを更新します。

反対に、Discriminatorは、できるだけGeneratorの画像を本物だと判定しないように、重みを更新します。

しくみとしてはこれだけで構成されていて、DCGANではGeneratorに逆Convolution（Deconvolution）を、DiscriminatorにConvolutionを用います。またConvolutionを行う際、BatchNormalizationを行うことで、高速な学習を可能にします。

実装する

今回はChainerを用いて、DCGANを実装しました。コードはgithubに置いています。https://github.com/Nyker510/hobby

僕のローカル環境ではGPUを使うことができないので、cpuを用いたコードになっていますので、そのまま使うととても遅いのでそれだけは注意してください。

構成としてはGenerator,Discriminatorを定義しているdcgan.pyとデータを与えて最適化していくtrainer.pyで構成されています。

dcgan.py

まずはGeneratorから

class Generator(Chain):
    '''ランダムなベクトルから画像を生成する画像作成機
    '''

    def __init__(self, z_dim):
        super(Generator, self).__init__(
            l1=L.Linear(z_dim, 3 * 3 * 512),

            dc1=L.Deconvolution2D(512, 256, 2, stride=2, pad=1,),
            dc2=L.Deconvolution2D(256, 128, 2, stride=2, pad=1,),
            dc3=L.Deconvolution2D(128, 64, 2, stride=2, pad=1,),
            dc4=L.Deconvolution2D(64, 1, 3, stride=3, pad=1),

            # Convolution, Deconvolutionともに値は画像の大きさに合わせて変化させる
            # 必要がある。

            # 今回はMNISTをターゲットにするので、元の大きさは28×28
            # 元の512チャンネルから1チャンネル（MNISTは白黒なためチャンネルが無い）に変換するまでに
            # 3→4→5→10→28となるようにstride,pad,windowの大きさを選んでいる

            #             bn0 = L.BatchNormalization(6*6*512),
            bn1=L.BatchNormalization(512),
            bn2=L.BatchNormalization(256),
            bn3=L.BatchNormalization(128),
            bn4=L.BatchNormalization(64),
        )
        self.z_dim = z_dim

    def __call__(self, z, test=False):
        h = self.l1(z)
        # 512チャンネルをもつ、3*3のベクトルに変換する
        h = F.reshape(h, (z.data.shape[0], 512, 3, 3))

        h = F.relu(self.bn1(h, test=test))
        h = F.relu(self.bn2(self.dc1(h), test=test))
        h = F.relu(self.bn3(self.dc2(h), test=test))
        h = F.relu(self.bn4(self.dc3(h), test=test))
        x = self.dc4(h)
        return x

Generatorはランダムなz_dim次元ベクトルを受け取って画像として返す関数です。今回実験対称としてMNISTの白黒画像を用いることを想定しているので、最後画像として返すDeconvolution関数を(28,28)次元のチャンネル数1と鳴るように、stride,pad,windowの大きさを選んでいます。

なので、違う大きさの画像でやりたいという場合や、RGBのある画像（チャンネル数が3）でやりたいというときは、それに合わせて変化させる必要があります。

（例えばRGBでやりたいのであれば、 dc4=L.Deconvolution2D(64, 3, 3, stride=3, pad=1)です）

これと反対方向に、即ち画像を受け取って2値に写像する関数として、Discriminatorも定義します。

trainer.py

trainer.pyでは実際に最適化を行っていきます。

大切なところは、lossをどのように与えるか、の部分です。

  z = np.random.uniform(-1, 1, (batchsize, self.z_dim))
  z = z.astype(dtype=np.float32)
  z = Variable(z)

  x = self.gen(z)
  y1 = self.dis(x)

  # 答え合わせ
  # ジェネレーターとしては0と判別させたい（騙すことが目的）
  loss_gen = F.softmax_cross_entropy(
      y1, Variable(np.zeros(batchsize, dtype=np.int32)))

  # 判別機としては1(偽物)と判別したい
  loss_dis = F.softmax_cross_entropy(
      y1, Variable(np.ones(batchsize, dtype=np.int32)))

  # load true data form dataset
  idx = perm[i * batchsize:(i + 1) * batchsize]
  x_data = self.X[idx]
  x_data = Variable(x_data)

  y2 = self.dis(x_data)

  # 今度は正しい画像なので、0（正しい画像）と判別したい
  loss_dis += F.softmax_cross_entropy(
      y2,  Variable(np.zeros(batchsize, dtype=np.int32)))

仮定として、Discriminatorの二次元の出力の内、0次元目を正しい画像である確率、1次元目を間違った画像（Generatorによって作成された偽画像）である確率であるとします。

まずzを適当なランダムベクトルとして設定した後、それをGeneratorに渡すことで画像xを作成します。その後、xをDiscriminatorに渡して二次元のベクトルy1を得ます。

Generatorとしては、Discriminatorを騙すことが目的です。
言い換えると、この画像xをDiscriminatorに渡した時に「本物だ！」と思わせたいのです。したがって全てのy1が0次元目の値が大きくなって欲しいので、ロスとしてy1と0とのSOFTMAXを与えます。

反対にDiscriminatorとしては、この画像xをちゃんと偽物であると判定しなくてはなりません。
すなわち1次元目が大きい値を取るようになって欲しいので、Discriminatorのロストしてはy1と1とのSOFTMAXを与えます。

そしてつぎに,Discriminatorに正しい画像も与えてあげて、これをちゃんと正しい画像（つまり0）と判定してほしいので、y2と0とのSOFTMAXをロスに加えます。

実験結果

MNISTの画像を使って実験を行います。本当は0~9でやれば一番良いのですが、GPUが使えない環境なので無限に時間がかかって終わりません。ですので泣く泣く、0の画像だけを用いて実験を行いました。

training中、epochが終わるごとにランダムなベクトルから画像をGeneratorによって作成してプロットさせていて、その画像を示します。同時にDiscriminatorが出力した「この画像が本物である確率」も画像の上に表示しています。

1 epoch目

ただのノイズです。

100 epoch目

だいぶ画像っぽくなってきました。がしかしDiscriminatorには正しい画像だとは思われていないようです。

500 epoch目

かなりしっかりと0を作るようになっています。正しい画像である確率が0.3程度になるなど、Discriminatorも判定に苦労している様子が伺えます。

1000 epoch目

500epoch目に比べて白黒の部分がはっきりとしてきました。

まとめ

今回はMNISTの0の画像だけというシンプルなタスクですが、学習が進むに連れて明確な輪郭をもって画像を出力する様子が確認できました。GPU環境であれば、更に高次の特徴をもった画像（例えばキャラクターのイラストなど）でも作成できるようなので、画像の自動生成技術として様々な用途で使えるかもしれません。

参考文献

• Chainerを使ってコンピュータにイラストを描かせる - Qiita
• TensorFlowによるDCGANでアイドルの顔画像生成 - すぎゃーんメモ

PRML 10章の変分ベイズ法の実装

線形回帰に対する変分法を用いた計算について実装してみました。

コードは以下から
github.com

変分ベイズではまず、隠れ変数も含めた完全データに対して同時分布を定義します。その後隠れ変数の分布が複数の関数の積として近似して表すことができる、という仮定を導入します。

このことによって、完全データに対する同時分布を、目的の隠れ変数以外の事後分布で周辺化したものが、新しい近似事後分布となり、それをすべての隠れ変数に対して繰り返して計算していくことにより、より尤度の高い隠れ変数の事後分布を計算していく、という手法です。

今回は次のグラフィカルモデルで表すことができる確率モデルに対して、変分ベイズ方を適用します。

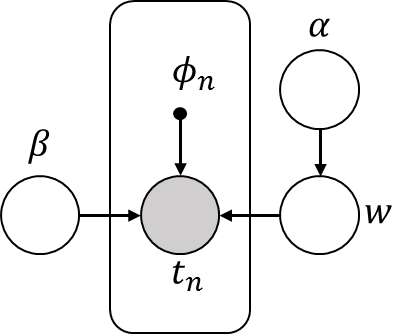
PRML10.3と似ていますが、実際のラベルデータが生成される際の精度パラメータβに対しても分布を定義している部分が異なっています。βに分布をもたせるとどのぐらい変化があるのかということを確かめたかったので、βにも分布をもたせました。

データとしては正しいsin関数にsigma=.5のガウスノイズを付加したデータを用います。

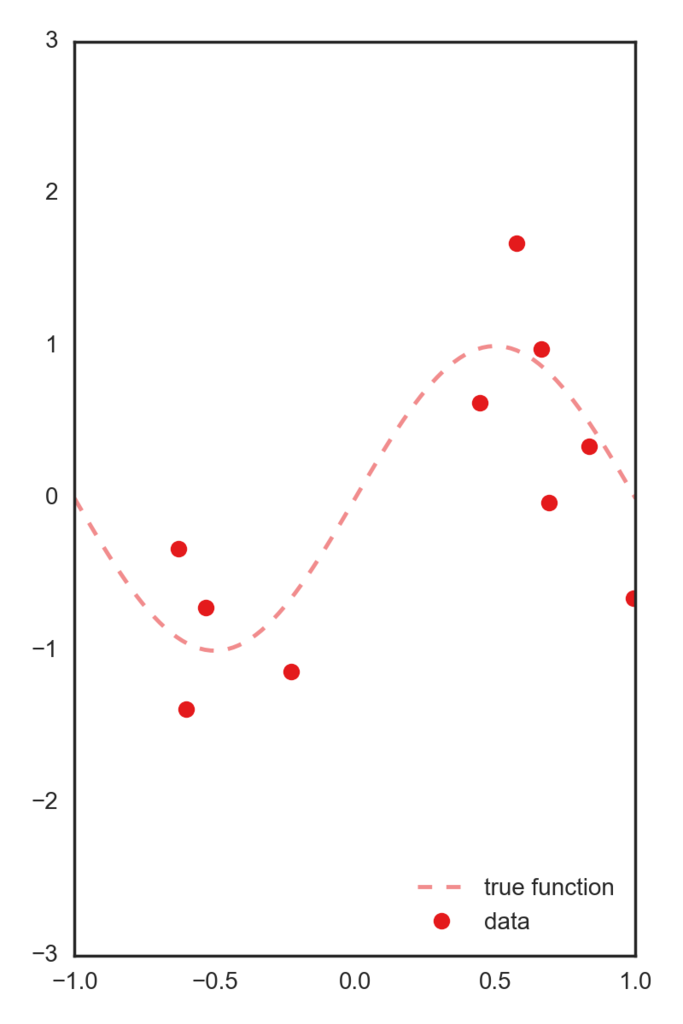
この一次元特徴を、[-1~1]を５個に分割した中心を持つガウス基底によって５次元空間に写像したデータを特徴量として用います。 以下コードです。

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

np.random.seed(71)


def t_func(x):
    """正解ラベルを作る関数
    x: numpy array.
    return t: target array. numpy.array like.
    """
    t = np.sin(x * np.pi)
    # t = np.where(x > 0, 1, -1)
    return t


def plot_target_function(x, ax=None, color="default"):
    """target関数（ノイズなし）をプロットします
    """
    if ax is None:
        ax = plt.subplot(111)
    if color is "default":
        color = "C0"
    ax.plot(x, t_func(x), "--", label="true function", color=color, alpha=.5)
    return ax


def phi_poly(x):
    dims = 3
    return [x ** i for i in range(0, dims + 1)]


def phi_gauss(x):
    bases = np.linspace(-1, 1, 5)
    return [np.exp(- (x - b) ** 2. * 10.) for b in bases]


def qw(alpha, phi, t, beta):
    """
    wの事後分布を計算します。
    変分事後分布はガウス分布なので決定すべきパラメータは平均と分散です
    w ~ N(w| m, S)
    return ガウス分布のパラメータ m, S
    """
    S = beta * phi.T.dot(phi) + alpha * np.eye(phi.shape[1])
    S = np.linalg.inv(S)
    m = beta * S.dot(phi.T).dot(t)
    return m, S


def qbeta(mn, Sn, t, Phi, N, c0, d0):
    """
    betaの変分事後分布を決めるcn,dnを計算します
    変分事後分布はガンマ分布なので決定すべきパラメータは2つです
    beta ~ Gamma(beta | a, b)
    return ガンマ分布のパラメータ a,b
    """
    cn = c0 + .5 * N
    dn = d0 + .5 * (np.linalg.norm(t - Phi.dot(mn)) **
                    2. + np.trace(Phi.T.dot(Phi).dot(Sn)))
    return cn, dn


def qalpha(w2, a0, b0, m):
    """
    alphaの変分事後分布を計算します。
    変分事後分布はガンマ分布ですから決定すべきパラメータは2つです
    alpha ~ Gamma(alpha | a, b)
    return a, b
    """
    a = a0 + m / 2.
    b = b0 + 1 / 2. * w2
    return a, b


def fit(phi_func, x, update_beta=False):
    xx = np.linspace(-2, 2., 100)
    if phi_func == "gauss":
        phi_func = phi_gauss
    elif phi_func == "poly":
        phi_func == phi_poly
    else:
        if type(phi_func) == "function":
            pass
        else:
            raise Exception("invalid phi_func")
    Phi = np.array([phi_func(xi) for xi in x])
    Phi_xx = np.array([phi_func(xi) for xi in xx])

    # 変分事後分布の初期値
    N, m = Phi.shape
    mn = np.zeros(shape=(Phi.shape[1],))
    Sn = np.eye(len(mn))
    beta = 10.
    alpha = .1
    a0, b0 = 1, 1
    c0, d0 = 1, 1

    pred_color = "C1"

    freq = 2
    n_iter = 3 * freq
    n_fig = int(n_iter / freq)

    fig = plt.figure(figsize=(3 * n_fig, 4))
    data_iter = []
    data_iter.append([alpha, beta])

    for i in range(n_iter):
        print("alpha:{alpha:.3g} beta:{beta:.3g}".format(**locals()))

        mn, Sn = qw(alpha, Phi, t, beta)
        w2 = np.linalg.norm(mn) ** 2. + np.trace(Sn)
        a, b = qalpha(w2, a0, b0, m)
        c, d = qbeta(mn, Sn, t, Phi, N, c0, d0)

        alpha = a / b

        if update_beta:
            # betaが更新される
            beta = c / d

        data_iter.append([alpha, beta])

        if i % freq == 0:
            k = int(i / freq) + 1
            ax_i = fig.add_subplot(1, n_fig, k)
            plot_target_function(xx, ax=ax_i)
            ax_i.plot(x, t, "o", label="data", alpha=.8)

            m_line = Phi_xx.dot(mn)
            sigma = (1. / beta + np.diag(Phi_xx.dot(Sn).dot(Phi_xx.T))) ** .5
            ax_i.plot(xx, m_line, "-", label="predict-line", color=pred_color)
            ax_i.fill_between(xx, m_line + sigma, m_line - sigma, label="Predict 1 sigma", alpha=.2, color=pred_color)
            ax_i.set_title(
                "n_iter:{i} alpha:{alpha:.3g} beta:{beta:.3g}".format(**locals()))
            ax_i.set_ylim(-2, 2)
            ax_i.set_xlim(-1.5, 1.5)
        if i == 0:
            ax_i.legend(loc=4)

    fig.tight_layout()
    return fig, data_iter

まずはβを更新せずハイパーパラメータとして与えて、変分ベイズを適用します。(β=10で固定)
一番左が初期値での最尤推定値となっていて、右に行くほど変分ベイズ法によって更新された分布情報に基づいた予測値になっています。今回与えたβが、実際の精度パラメータよりも大きな値を取っているために、データ点に過剰にフィットしていることが伺えます。

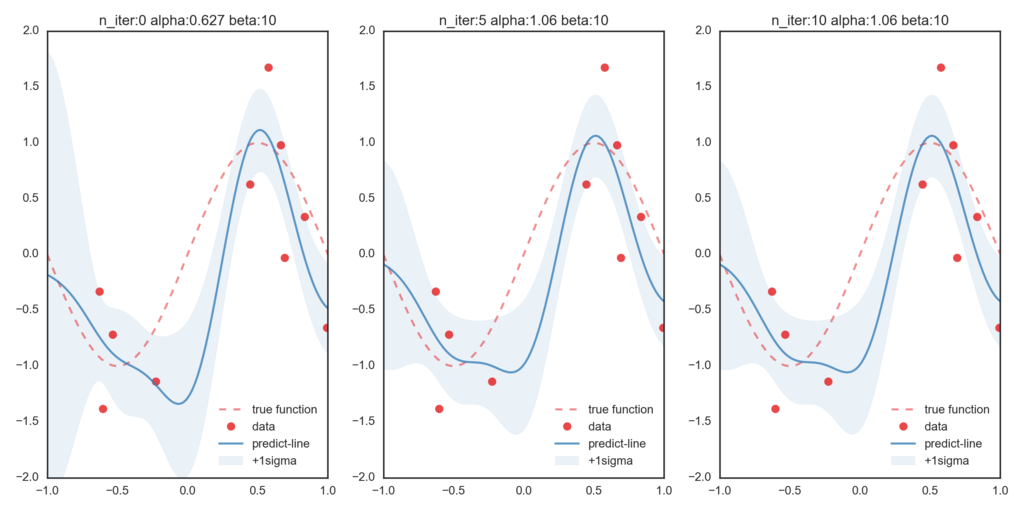
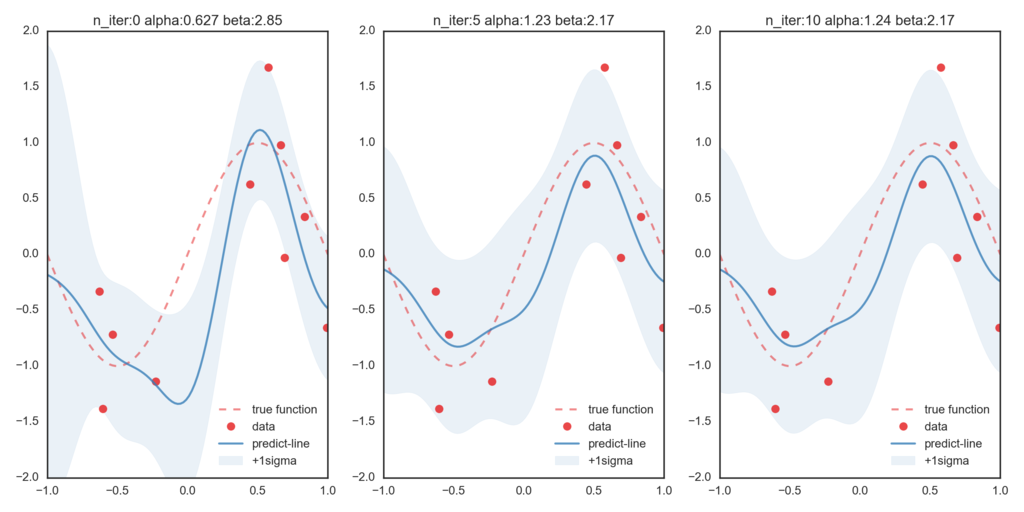
つぎにβを変分ベイズ法で更新したのが次のグラフです。比べてみると、βが更新されることによって正しい関数に近づいていることが確認できます。

format記法の使い道

pythonでは変数の情報を文字列にする方法がいくつかありますが、その中でも僕はformat記法をよく使っています。

特に最近「dictionaryを文字列にしたいなぁ」という場合に、とてもきれいに書くことができるということを発見（というかドキュメントを読んで判明した）ので「こういう場合に便利ですよ」という意味合いでメモしておきます。

Case: dictionaryからstringに変換したい

例えば、機械学習なんかをやろうと思うと、パラメータをディクショナリとして渡す場面がよくあると思います。仮にそのパラメータをparamsとして以下のように定義します。

params = {
    'estimator':'svm',
    'gamma':0.1,
    'eta':100,
}

このパラメータを使って学習した結果を保存しよう、となると「このパラメータ使いましたよ」という名前で保存したくなります。そういうときにdictionary→stringに変換したくなります。

単純に要素をすべて列挙してそれをつなげる、という風にすると以下のようなプログラムが考えられます。

pstr = ''
for key,val in params.items():
    if pstr != '':
        pstr += '_'
    pstr += key + '-' +str(val)
print(pstr) # <<< 'estimator-svm_eta-100_gamma-0.1'

これでいいように感じるのですが、一つ問題があります。

dictionaryは入っている要素の順番を保存していないので、実験を繰り返しているとタイトルの順番が変化してしまう場合があるのです。（実際にあってとても困りました）

'estimator-svm_eta-100_gamma-0.1' これが 'eta-100_estimator-svm_gamma-0.1' こんな風になる場合があるってこと

また先のスクリプトでは辞書の値をすべてstrを用いて文字に変換しています。これも問題があって、例えばfloatをstrを用いて文字にすると桁数の指定ができないのでstr(val)[:2]のようにして長さを揃えたりしなくてはならず、しかもこれをすると四捨五入等も行ってくれないので、まあ言ったらちょっと不便です。

そこで最近はformat記法を用いて文字列に変換するようにしています。

estimator = 'svm'
gamma = 0.166
eta = 100
pstr = 'estimator-{0}_gamma-{1:.2f}_eta-{2}'.format(estimator,gamma,eta)

print(pstr) # estimator-svm_gamma-0.17_eta-100

{}の中の番号がformatで与えた引数の順番に対応しています。また同時にそれをどういう形でstrにするかも指定できるので、先の例だとgammaを下二桁の少数で、という指定をしているので0.17として出力されています。

これでもだいぶ便利なのですが、コードを書いていて「新しい変数hogeも名前の先頭に追加したいなー」となったとき、先頭にhogeを追加すると、順番がひとつづつずれてしまうので、0,1,2を1,2,3にしなくてはならなくなり、面倒です。

これを回避するためには、最後にhogeを追加して、3番めの引数を文字列の先頭に持ってくる、というformat内部の並びと、文字の対応が取れないコードになってしまいます。ちょっとアホっぽいですね。

hoge = 0.2
estimator = 'svm'
gamma = 0.166
eta = 100
pstr = 'hoge-{3:.3f}_estimator-{0}_gamma-{1:.2f}_eta-{2}'.format(estimator,gamma,eta,hoge)

print(pstr) # hoge-0.200_estimator-svm_gamma-0.17_eta-100

辞書の展開わたし

これを回避するのが、辞書を展開して渡してあげる、という方法です。(format(**some_dict))

展開した辞書の値をほしいときには{key}としてあげます。具体的には一番最初の例だとこんな感じ。

pstr = 'estimator-{estimator}'.format(**params)
print(pstr) # estimator-svm

この書き方の良い点は、stringの中にkeyを書くことになるので、ぱっと見たときにこの文字列が何になるのか、がわかりやすいという点です。

短所として長くなると手で書いているのが面倒になるという点がありますが、それでも読みやすいわかりやすいというメリットは大きいと思います。

しかしこの方法は文字にしたいものが最初からdictionaryになっている場合にしか使えません。

locals()

なのですが、これと組み込み関数のlocals()を用いるとその場合でも楽に変換できます。

localsはその場に定義されている変数を辞書にして返す関数です。なのでこれとformatを組み合わせると、その場にある変数の文字列を先の記法で作ることができます。

val = 100
name = 'some_method'

tstr = 'val={val}_name={name}'.format(**locals())
print(tstr) # val=100_name=some_method

0,1,2と指定する場合に比べて、明らかに見やすいですね。

まとめ

localsとか展開渡しとか全然知らずにアホっぽいコード量産していました。ドキュメントはちゃんと読みましょう。